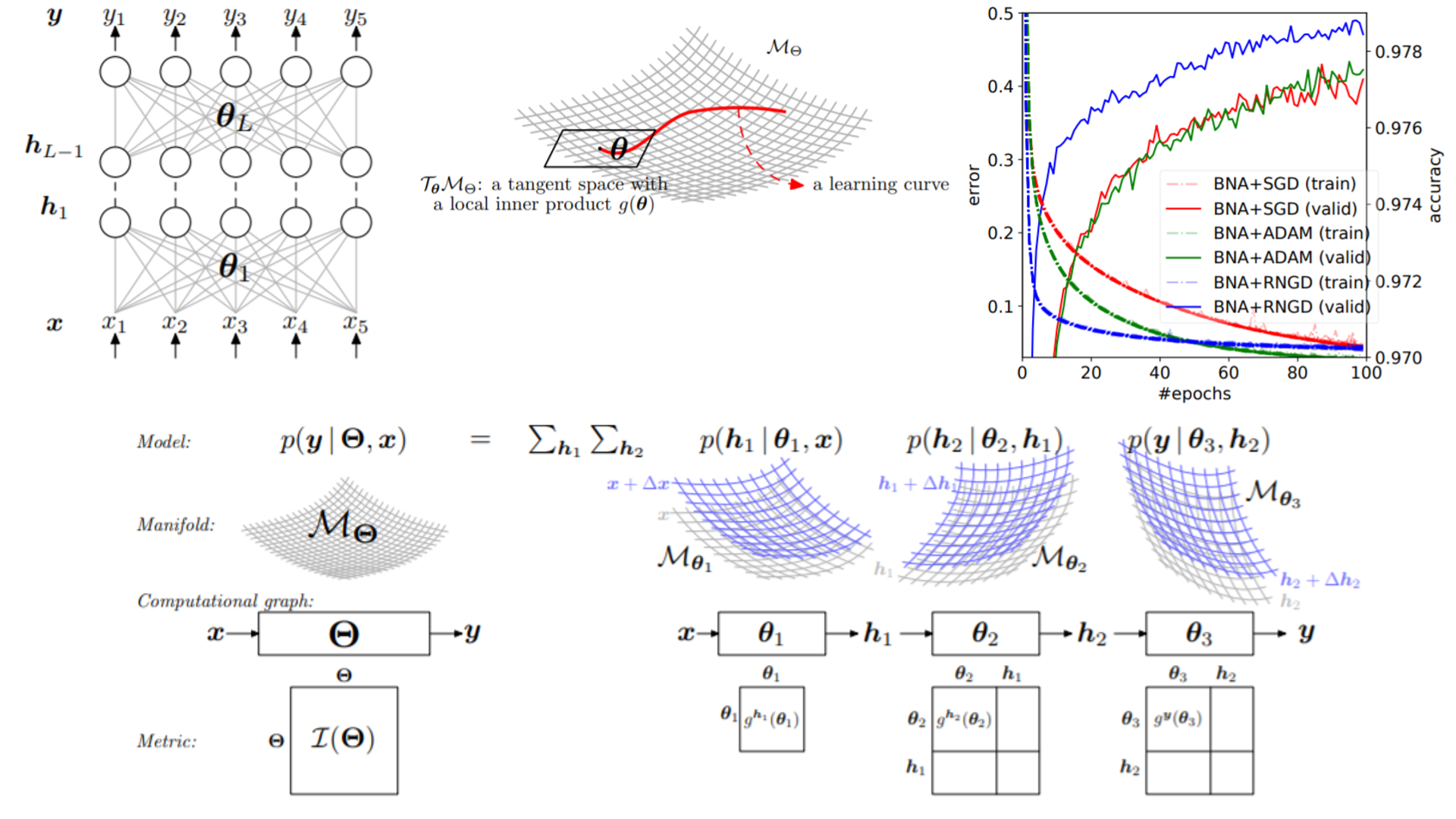
Information geometry and divergences: Classical and Quantum
Foundations, Applications, and Software APIs
Historically, Information Geometry (IG, tutorials,
textbooks and monographs and how to get started) aimed at unravelling the geometric structures
of families of probability distributions called the statistical models.
A statistical model can either be
- parametric (eg., family of normal distributions),
- semi-parametric
(eg., family of Gaussian mixture models) or
- non-parametric (family of mutually absolutely continuous smooth densities).
A parametric statistical model is said regular when the Fisher information matrix is positive-definite (and well-defined).
Otherwise, the statistical model is irregular (eg., infinite Fisher information and semi-positive definite Fisher information when the model is not identifiable).
The Fisher-Rao manifold of a statistical parametric model
is a Riemannian manifold equipped
with the Fisher information metric.
The geodesic length on a Fisher-Rao manifold is called Rao's distance [Hotelling 1930]
[Rao 1945].
More generally, Amari proposed the dualistic structure of IG which consists
of a pair of torsion-free affine connections coupled to the Fisher metric [Amari 1980's].
Given a dualistic structure, we can build generically a one-parameter family of
dualistic information-geometric structures,
called the α-geometry.
When both connections are flat, the information-geometric space is said dually flat:
For example, the Amari's ±1-structures of exponential families and mixture families
are famous examples of dually flat spaces in information geometry.
In differential geometry, geodesics are defined as autoparallel curves with respect to a connection.
When using the default Levi-Civita metric connection derived from the Fisher metric on Fisher-Rao manifolds,
we get Rao's distance which are locally minimizing geodesics.
Eguchi showed how to build from any smooth distortion (originally called a contrast function)
a dualistic structure: The information geometry of divergences [Eguchi 1982].
The information geometry of Bregman divergences yields dually flat spaces:
It is a special cases of Hessian manifolds which are differentiable manifolds
equipped with a metric tensor being a Hessian metric and a flat connection [Shima 2007].
Since geometric structures scaffold spaces independently of any applications,
these pure information-geometric Fisher-Rao structure and α-structures of statistical models
can also be used in non-statistical contexts too:
For example, for analyzing interior point methods with barrier functions in optimization, or for studying time-series models, etc.
Statistical divergences between parametric statistical models amount to
parameter divergences on which we can use the Eguchi's divergence information geometry
to get a dualistic structure.
A projective divergence is a divergence which is invariant by independent rescaling of its parameters.
A statistical projective divergence is thus useful for estimating computationally
intractable statistical models (eg., gamma divergences, Cauchy-Schwarz divergence and Hölder divergences, or singly-sided projective Hyvärinen divergence).
A conformal divergence is a divergence scaled by a conformal factor which may depend on one or two of its arguments.
The metric tensor obtained from Eguchi's information divergence of a conformal divergence
is a conformal metric of the metric obtained from the divergence, hence its name.
By analogy to total least squares vs least squares, a
total divergence is a divergence which is invariant wrt. to rotations (eg., total Bregman divergences).
An important property of divergences on the probability simplex is to be monotone by coarse-graining.
That is, merging bins and considering reduced histograms should give a distance less or equal than the distance on the full resolution histograms.
This information monotonicity property holds for f-divergences (called invariant divergences in information geometry),
Hilbert log cross-ratio distance, or Aitchison distance for example.
Some statistical divergences are upper bounded
(eg., Jensen-Shannon divergence) while others are not (eg., Jeffreys' divergence).
Optimal transport distances require a ground base distance on the sample space.
A diversity index generalizes a two-point distance to a family of parameters/distributions.
It usually measures the dispersion around a center point (eg., like variance measures
the dispersion around the centroid).
A selected list of ten great articles in information geometry introducing various concepts like statistical invariance, divergences, dual geometric structures, information projections, dual foliations, information decomposition, mixed coordinates, etc.
Browsing geometric structures:
[tutorials]
[Software/API]
[Fisher-Rao manifolds]
[Cones]
[Finsler manifolds]
[Hessian manifolds]
[Exponential families and mixture families]
[Categorical distributions/probability simplex]
[Time series]
[Hilbert geometry]
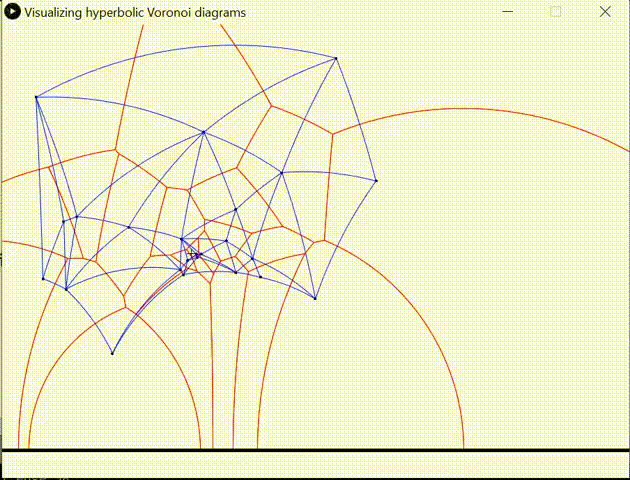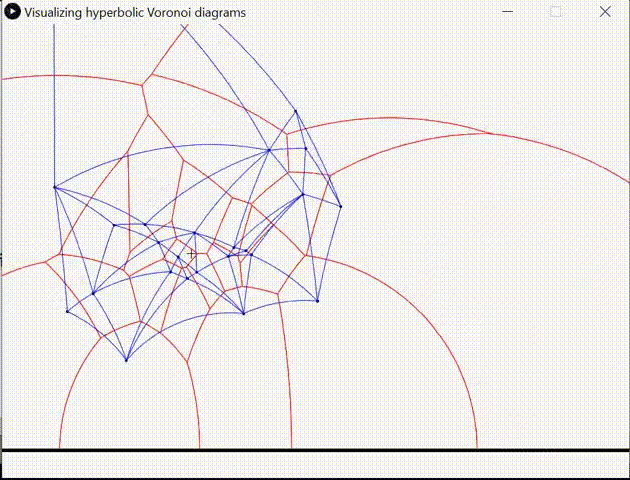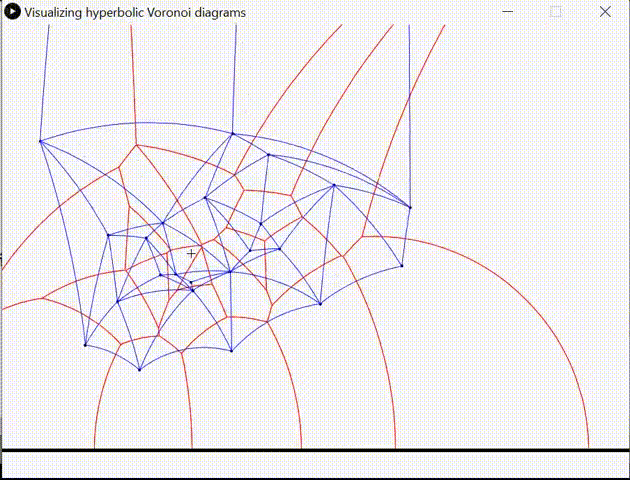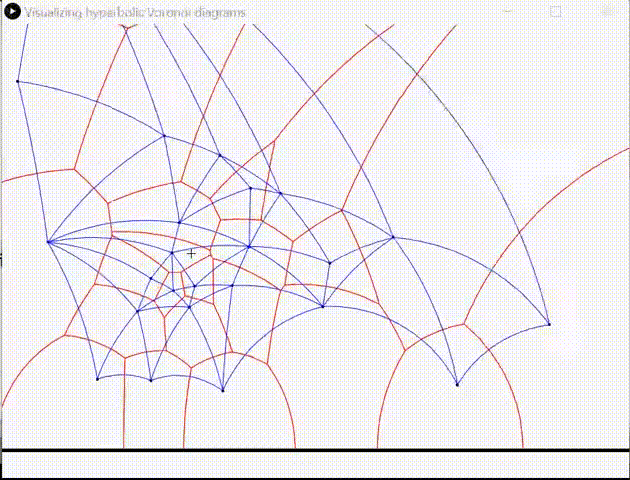
[Hyperbolic geometry and Siegel spaces]
[Applications]
[Natural gradient]
[centroids and clustering]
[Miscellaneous applications]
Browsing [Dissimilarities]:
[Jensen-Shannon divergence]
[f-divergences]
[Bregman divergences]
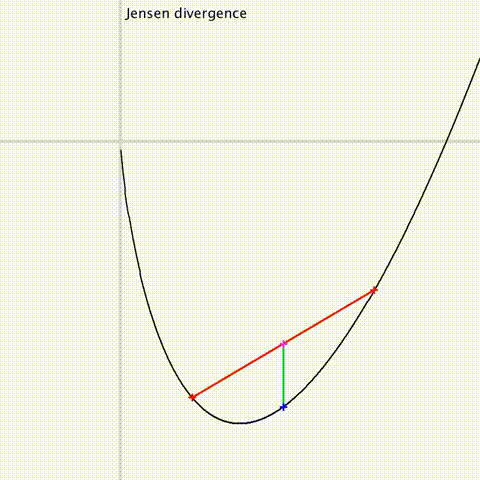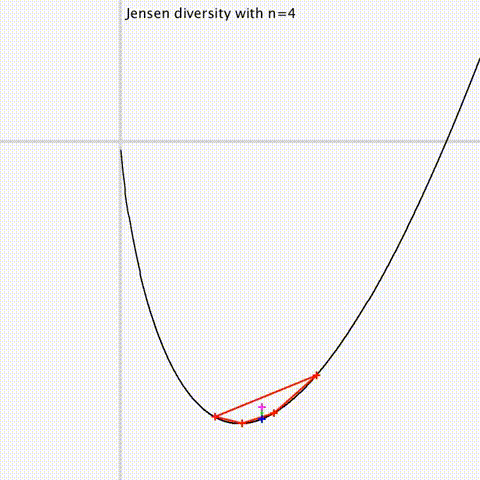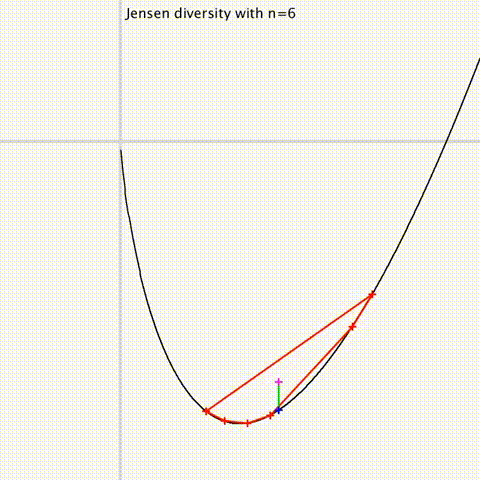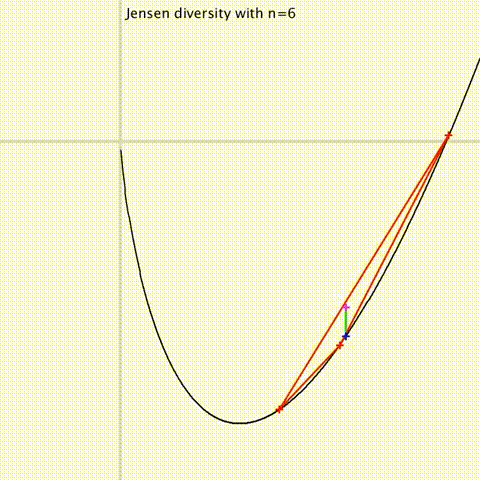
[Jensen divergences]
[conformal divergences]
[projective divergences]
[optimal transport]
[entropies]
[Chernoff information]
Information geometry: Tutorials and surveys
 The Many Faces of Information Geometry, AMS Notices (9 pages), 2022.
The Many Faces of Information Geometry, AMS Notices (9 pages), 2022.
A gentle short introduction to information geometry

- An Elementary Introduction to Information Geometry, Entropy (61 pages), 2020.
A self-contained introduction to classic parametric information geometry with applications and basics of differential geometry


- What is an information projection?, AMS Notices, (65) 3 (4 pages), 2018.
Information projections are the workhorses of algorithms using the framework of information geometry.
A projection is defined according to geodesics (wrt a connection) and orthogonality (wrt a metric tensor).
In dually flat spaces, information projections can be interpreted as minimum Bregman divergences (Bregman projections).
Unicity theorems for exponential families and mixture families.

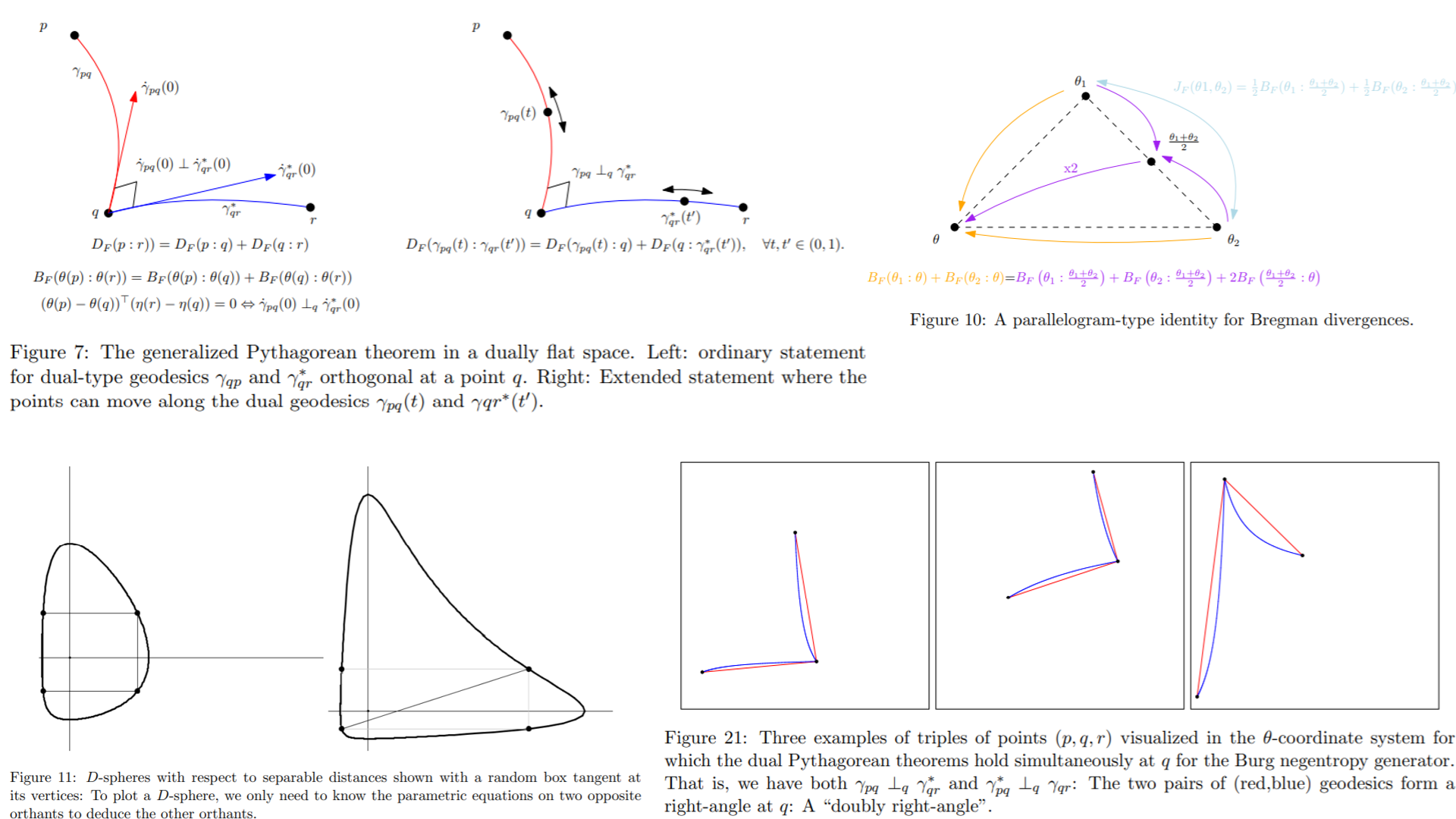
- On Geodesic Triangles with Right Angles in a Dually Flat Space, Chapter in edited book "Progress in Information Geometry", Springer, 2021.
A self-contained introduction to dually flat spaces which we call Bregman manifolds. The generalized Pythagorean theorem is derived from the 3-parameter Bregman identity.
The 4-parameter Bregman identity is also explained
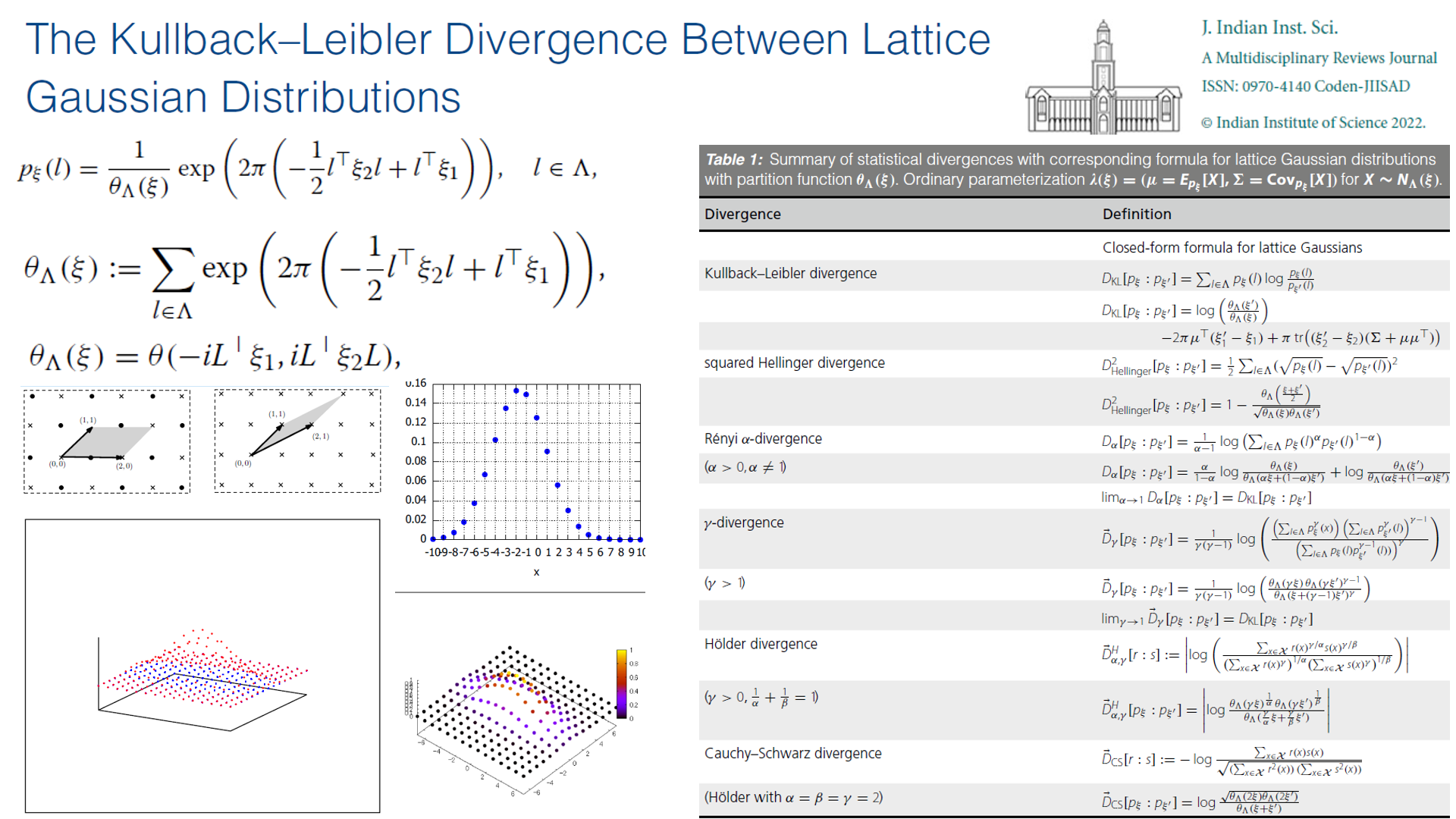
- Cramér-Rao Lower Bound and Information Geometry, Connected at Infinity II: On the work of Indian mathematicians (R. Bhatia and C.S. Rajan, Eds.), special volume of Texts and Readings In Mathematics (TRIM), Hindustan Book Agency, 2013
A description of the pathbreaking paper of Calyampudi Radhakrishna Rao (1945): "Information and the accuracy attainable in the estimation of statistical parameters", 1945.

-
Statistical exponential families: A digest with flash cards, 2009

-
Pattern Learning and Recognition on Statistical Manifolds: An Information-Geometric Review, SIMBAD 2013

- Legendre transformation and information geometry, memo, 2010
Fisher-Rao manifolds (Riemannian manifolds and Hamadard manifolds)
Cones
Finsler manifolds
Finsler manifolds are proposed to model irregular parametric statistical models (where Fisher information can be infinite)
Bregman manifolds/Hessian manifolds
Exponential families and Mixture families
Continuous or discrete exponential families
Online k-MLE for Mixture Modeling with Exponential Families, GSI 2015
k-MLE: A fast algorithm for learning statistical mixture models, IEEE ICASSP 2012
 Fast Learning of Gamma Mixture Models with k-MLE, SIMBAD 2013: 235-249
k-MLE for mixtures of generalized Gaussians,
ICPR 2012: 2825-2828
Simplification and hierarchical representations of mixtures of exponential families,
Signal Process. 90(12): 3197-3212 (2010)
Fast Learning of Gamma Mixture Models with k-MLE, SIMBAD 2013: 235-249
k-MLE for mixtures of generalized Gaussians,
ICPR 2012: 2825-2828
Simplification and hierarchical representations of mixtures of exponential families,
Signal Process. 90(12): 3197-3212 (2010)
 The analytic dually flat space of the statistical mixture family of two prescribed distinct Cauchy components
On the Geometry of Mixtures of Prescribed Distributions, IEEE ICASSP 2018
The analytic dually flat space of the statistical mixture family of two prescribed distinct Cauchy components
On the Geometry of Mixtures of Prescribed Distributions, IEEE ICASSP 2018
Information geometry of deformed exponential families
q-deformed exponential families, q-Gaussians, etc.
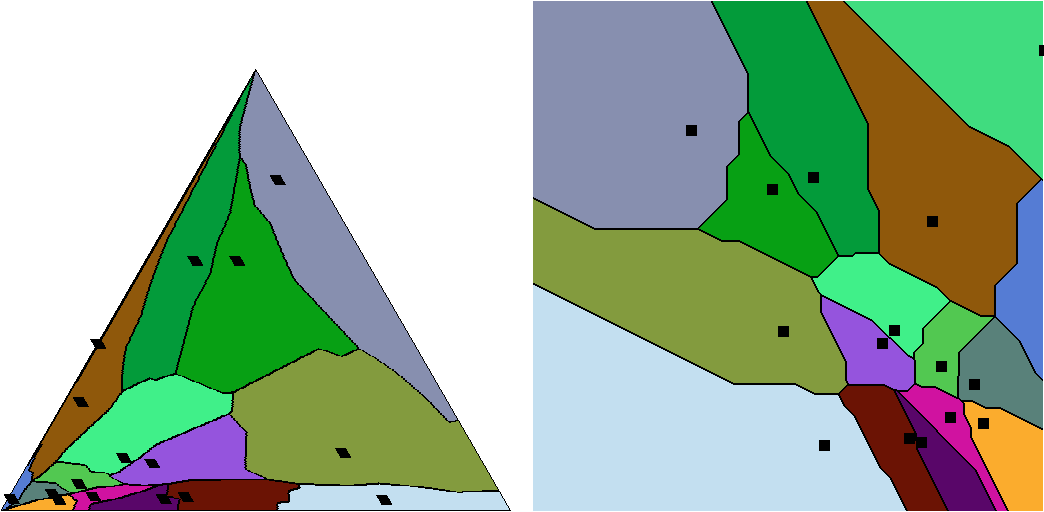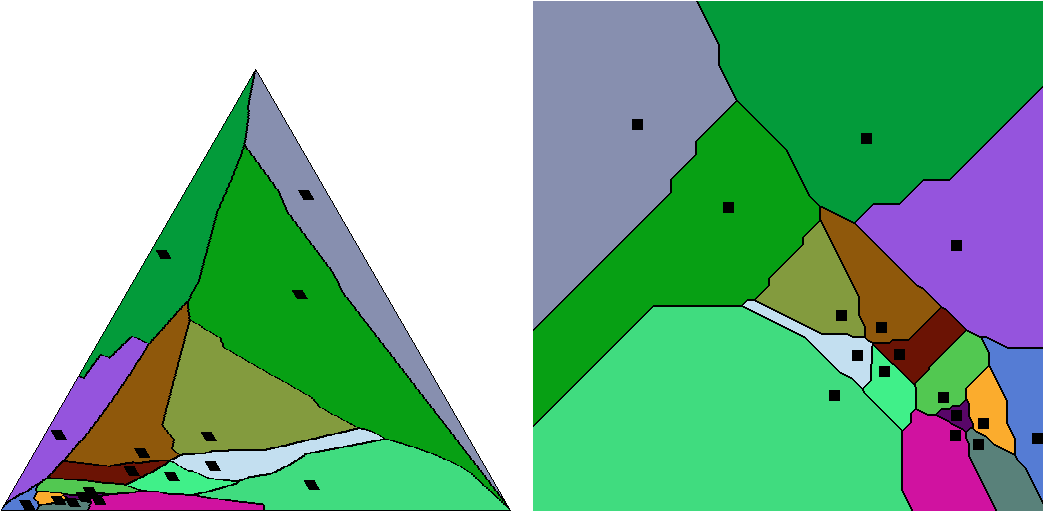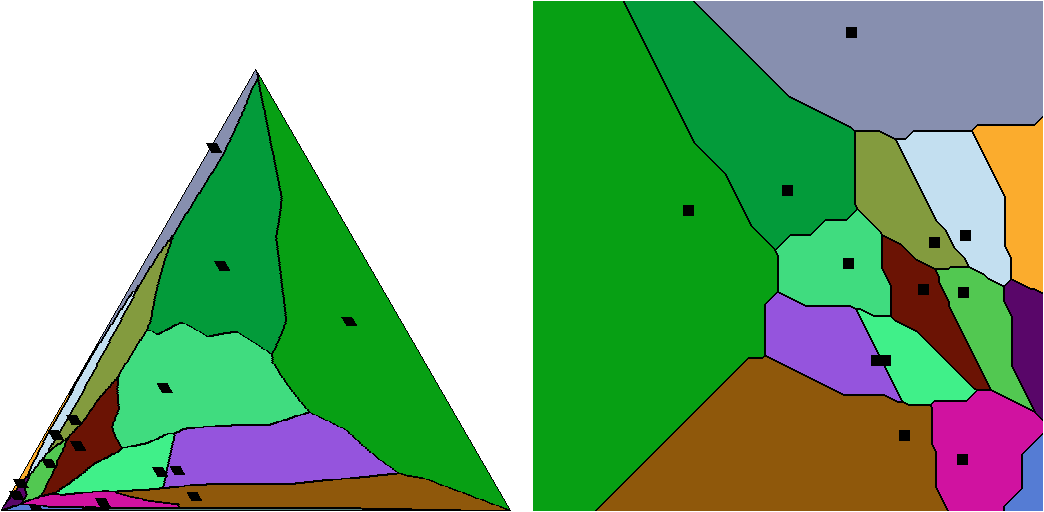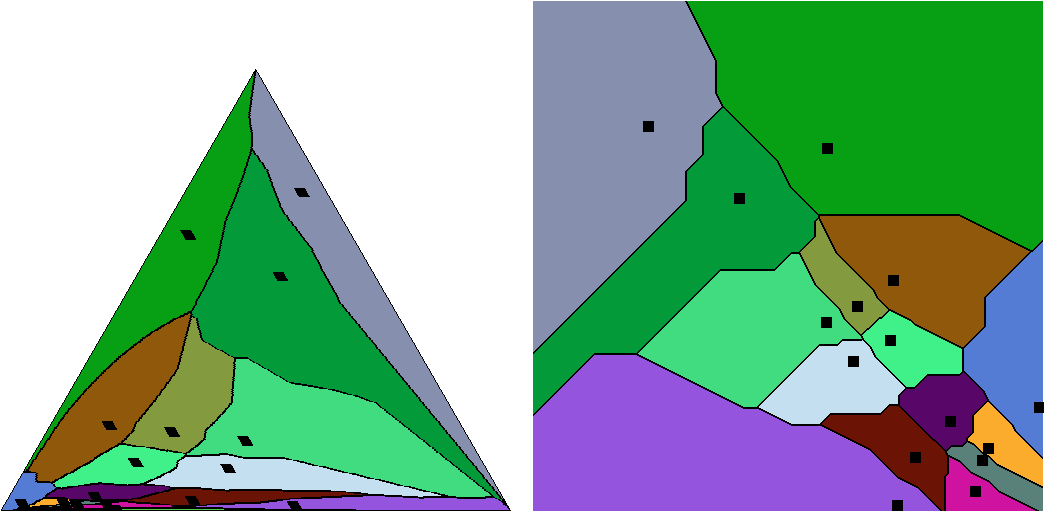
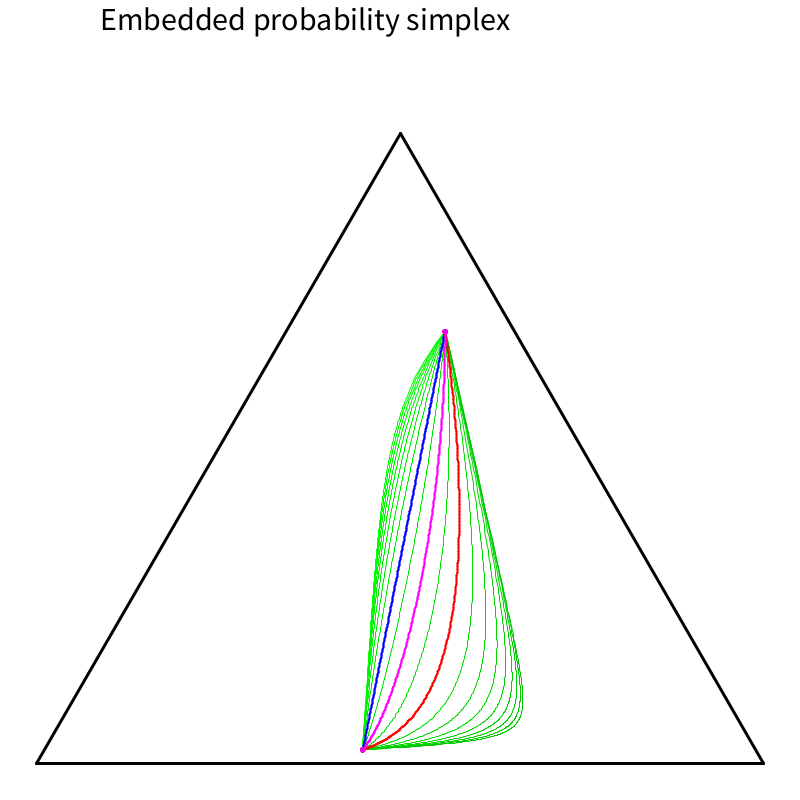
Information geometry of the probability simplex
Clustering in Hilbert simplex geometry
[project page]
Geometry of the probability simplex and
its connection to the maximum entropy method,
Journal of Applied Mathematics, Statistics and Informatics 16(1):25-35, 2020
Bruhat-Tits space
open access (publisher)
Information geometry of singular statistical models
 A Geometric Modeling of Occam's Razor in Deep Learning
A Geometric Modeling of Occam's Razor in Deep Learning
 Towards Modeling and Resolving Singular Parameter Spaces using Stratifolds, Neurips OPT workshop 2021
Towards Modeling and Resolving Singular Parameter Spaces using Stratifolds, Neurips OPT workshop 2021
Geometry of time series and correlations/dependences
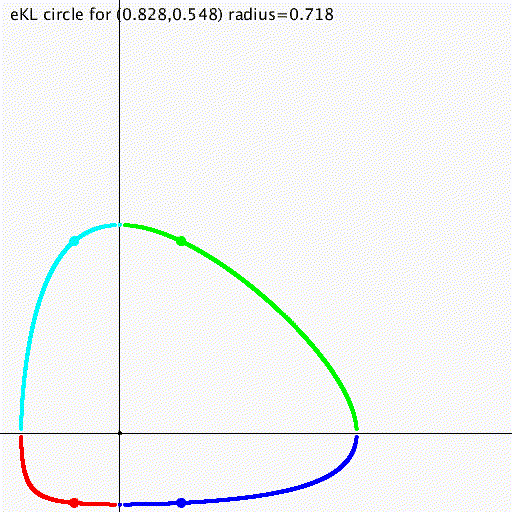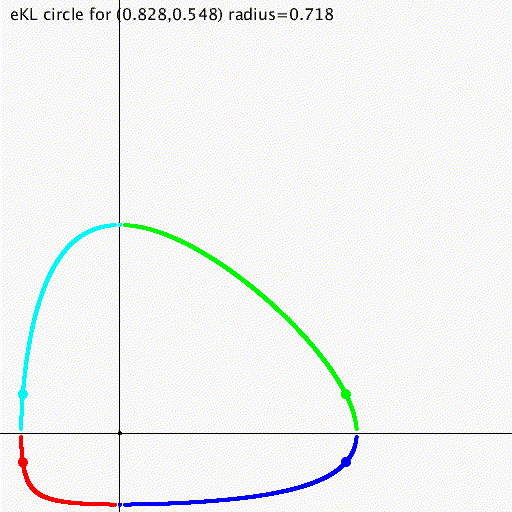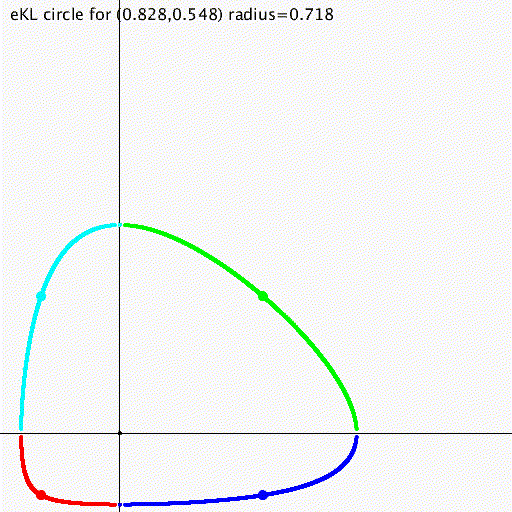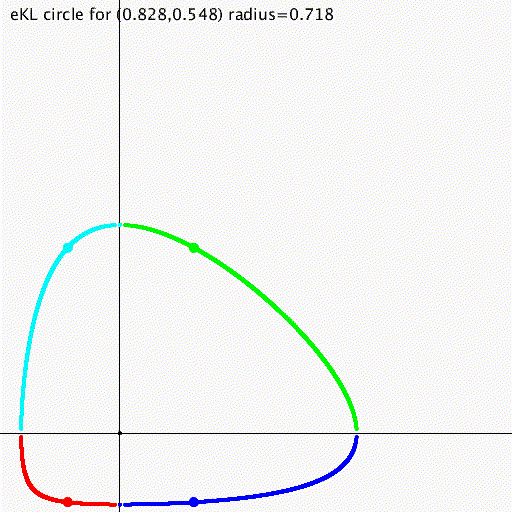
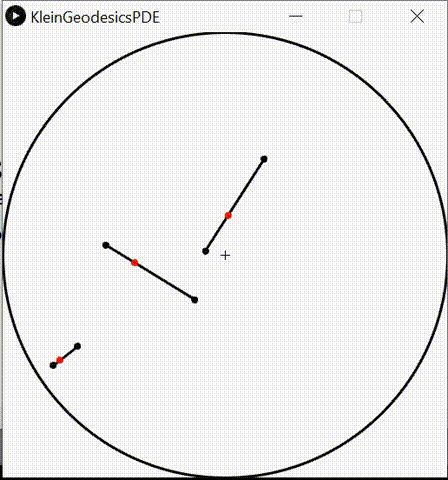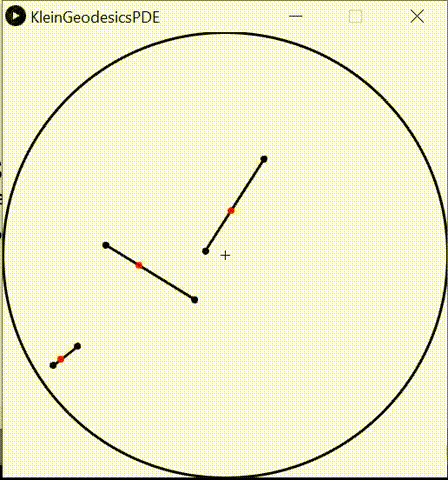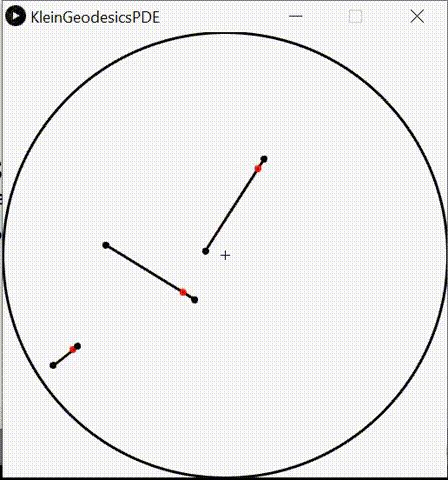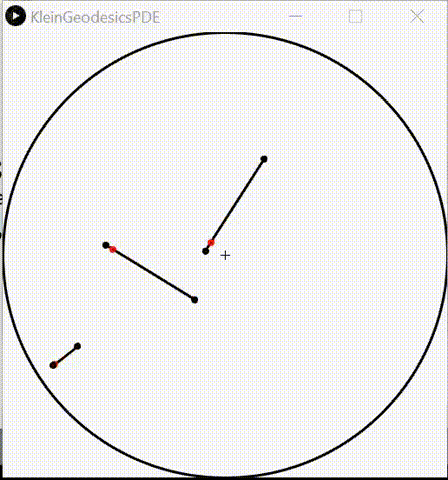
Hilbert geometry
Hilbert geometry are induced by a bounded convex open domain.
Hilbert geometry generalize the Klein model of hyperbolic geometry and the Cayley-Klein geometry
Beware that Hilbert geometry are never Hilbert spaces!
Hyperbolic geometry and geometry of Siegel domains
Some applications of information geometry
Natural gradient
Centers and clustering
Miscellaneous applications
Dissimilarities, distances, divergences and diversities
Jensen-Shannon divergence
Probability simplex
f-divergences
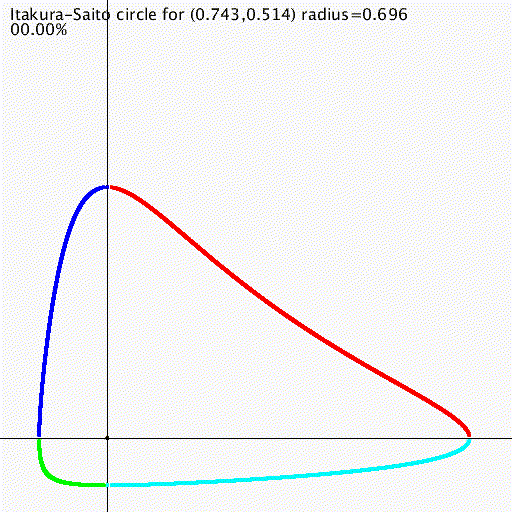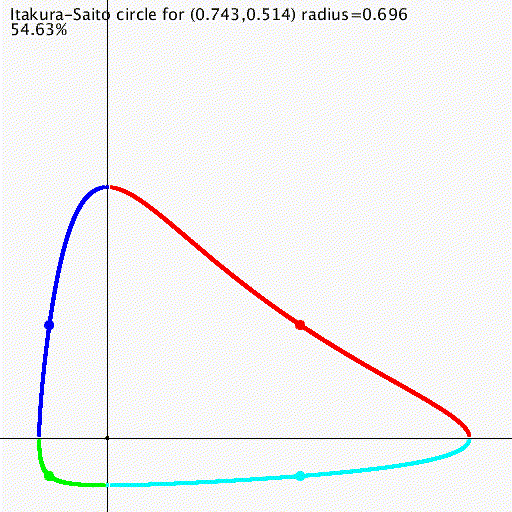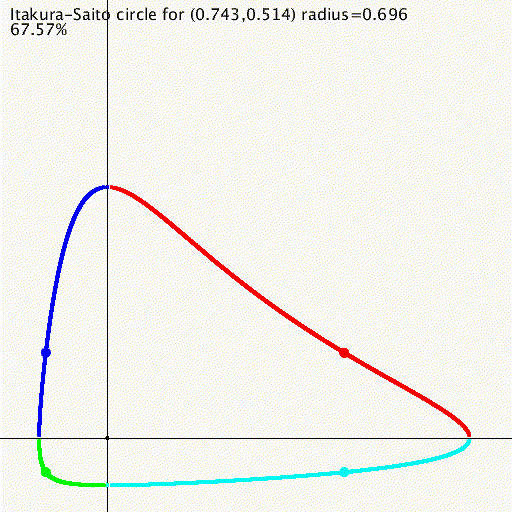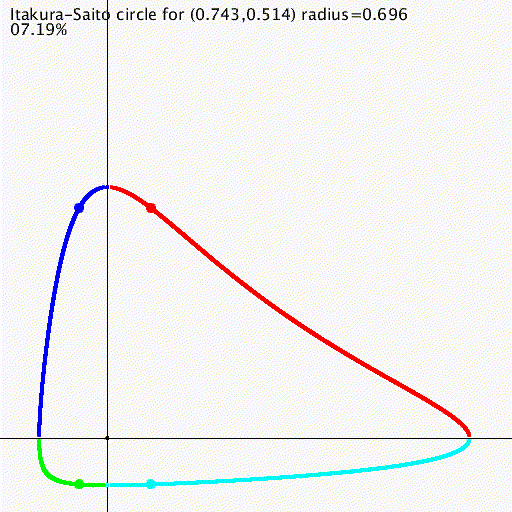
Bregman divergences and some generalizations
 Statistical Divergences between Densities of Truncated Exponential Families with Nested Supports: Duo Bregman
and Duo Jensen Divergences, Entropy 2022, 24(3)
Statistical Divergences between Densities of Truncated Exponential Families with Nested Supports: Duo Bregman
and Duo Jensen Divergences, Entropy 2022, 24(3)
Duo Fenchel-Young divergence , arXiv:2202.10726.
We define duo Bregman divergences, duo Fenchel-Young divergences, duo Jensen divergences.
We show how those divergences occur naturally when calculating the Kullback-Leibler divergence and
skew Bhattacharyya distances between densities belonging to nested exponential families.
We report the KLD between truncated normal distributions as a duo Bregman divergence.
Demo code:
Jensen divergences and some generalizations
Conformal divergences
Projective divergences
Optimal transport/Wasserstein distances/Sinkhorn distances
Earth mover distances (EMD), Wasserstein distances
-
Sinkhorn AutoEncoders, UAI 2019
-
On The Chain Rule Optimal Transport Distance, Progress in Information Geometry, 2021
-
Tsallis Regularized Optimal Transport and Ecological Inference, AAAI 2017
-
Clustering Patterns Connecting COVID-19 Dynamics and Human Mobility Using Optimal Transport,
March 2021, Sankhya B 83(S1)
-
Optimal copula transport for clustering multivariate time series, IEEE ICASSP 2016
-
Exploring and measuring non-linear correlations: Copulas, Lightspeed Transportation and Clustering,
Time Series Workshop at NeurIPS 2016
-
Earth Mover Distance on superpixels, IEEE ICIP 2010
Shannon, Rényi, Tsallis, Sharmal-Mittal entropies, cross-entropies and divergences
Chernoff information
Other dissimilarities
Loss functions and proper scoring rules
Divergences between statistical mixtures
-
Fast Approximations of the Jeffreys Divergence between Univariate Gaussian Mixtures
via Mixture Conversions to Exponential-Polynomial Distributions,
Entropy 2021, 23(11), 1417
-
The Statistical Minkowski Distances: Closed-Form Formula for Gaussian Mixture Models, GSI 2019
-
Guaranteed Deterministic Bounds on the total variation Distance between univariate mixtures, IEEE MLSP 2018
-
Comix: Joint estimation and lightspeed comparison of mixture models
, IEEE ICASSP 2016
-
Bag-of-Components: An Online Algorithm for Batch Learning of Mixture Models,
GSI 2015
-
Guaranteed Bounds on Information-Theoretic Measures of Univariate Mixtures Using Piecewise Log-Sum-Exp Inequalities
, Entropy 2016, 18(12), 442
-
Combinatorial bounds on the α-divergence of univariate mixture models, ICASSP 2017
-
Closed-form information-theoretic divergences for statistical mixtures, ICPR 2012
Edited books and proceedings
Monographs and textbooks on information geometry
 Geometry and Statistics (Handbook of Statistics, Volume 46),
Frank Nielsen, Arni Srinivasa Rao, C.R. Rao (2022)
Geometry and Statistics (Handbook of Statistics, Volume 46),
Frank Nielsen, Arni Srinivasa Rao, C.R. Rao (2022)
 https://link.springer.com/book/10.1007/978-981-33-6991-7
A Tribute to the Legend of Professor C. R. Rao:
The Centenary Volume. Editors: Arijit Chaudhuri, Sat N. Gupta, Rajkumar Roychoudhury
https://link.springer.com/book/10.1007/978-981-33-6991-7
A Tribute to the Legend of Professor C. R. Rao:
The Centenary Volume. Editors: Arijit Chaudhuri, Sat N. Gupta, Rajkumar Roychoudhury
 Methodology and Applications of Statistics
A Volume in Honor of C.R. Rao on the Occasion of his 100th Birthday.
Editors: Barry C. Arnold, Narayanaswamy Balakrishnan, Carlos A. Coelho
Methodology and Applications of Statistics
A Volume in Honor of C.R. Rao on the Occasion of his 100th Birthday.
Editors: Barry C. Arnold, Narayanaswamy Balakrishnan, Carlos A. Coelho
 Entropy, Divergence, and Majorization in Classical and Quantum Thermodynamics,
Takahiro Sagawa (2022)
Entropy, Divergence, and Majorization in Classical and Quantum Thermodynamics,
Takahiro Sagawa (2022)
 Minimum Divergence Methods in Statistical
Machine Learning: From an Information Geometric Viewpoint,
Shinto Eguchi, Osamu Komori (2022)
Minimum Divergence Methods in Statistical
Machine Learning: From an Information Geometric Viewpoint,
Shinto Eguchi, Osamu Komori (2022)
 Methodology and Applications of Statistics,
A Volume in Honor of C.R. Rao on the Occasion of his 100th Birthday,
Barry C. ArnoldNarayanaswamy BalakrishnanCarlos A. Coelho (Eds) (2021)
Methodology and Applications of Statistics,
A Volume in Honor of C.R. Rao on the Occasion of his 100th Birthday,
Barry C. ArnoldNarayanaswamy BalakrishnanCarlos A. Coelho (Eds) (2021)
 Information geometry, Arni S.R. Srinivasa Rao, C.R. Rao, Angelo Plastino (2020)
Information geometry, Arni S.R. Srinivasa Rao, C.R. Rao, Angelo Plastino (2020)
 Information geometry, Nihat Ay, Jürgen Jost, Hông Vân Lê, Lorenz Schwachhöfer (2017)
Information geometry, Nihat Ay, Jürgen Jost, Hông Vân Lê, Lorenz Schwachhöfer (2017)
Advanced and rigorous foundations of information geometry
 Information geometry and its applications, Shun-ichi Amari (2016)
Information geometry and its applications, Shun-ichi Amari (2016)
A first reading, well-balanced between concepts and applications by the founder of the field
 Riemannian Geometry and Statistical Machine Learning, Guy Lebanon, (2015)
Riemannian Geometry and Statistical Machine Learning, Guy Lebanon, (2015)
 Geometric Modeling in Probability and Statistics, Ovidiu Calin, Constantin Udrişte (2014)
Geometric Modeling in Probability and Statistics, Ovidiu Calin, Constantin Udrişte (2014)
 Finance At Fields by Matheus R Grasselli (Editor), Lane Palmer Hughston (Editor).
, https://doi.org/10.1142/8507, World Scientific, 2013. Mentions information geometry (p. 248)
Finance At Fields by Matheus R Grasselli (Editor), Lane Palmer Hughston (Editor).
, https://doi.org/10.1142/8507, World Scientific, 2013. Mentions information geometry (p. 248)
 Mathematical foundations of infinite-dimensional statistical models,
Richard Nickl and Evarist Giné,
Cambridge University Press (2016).
book web page (including book PDF)
Mathematical foundations of infinite-dimensional statistical models,
Richard Nickl and Evarist Giné,
Cambridge University Press (2016).
book web page (including book PDF)
A nice intermediate textbook which also give provides proofs using calculus on connections of differential geometry
 Methods of Information Geometry, Shun-ichi Amari, Hiroshi Nagaoka (2000)
Methods of Information Geometry, Shun-ichi Amari, Hiroshi Nagaoka (2000)
Advanced book with an emphasis on statistical inference,
english translation of the Japanese textbook of 1993
 Differential Geometry and Statistics, Michael K. Murray, John W. Rice (1993)
Differential Geometry and Statistics, Michael K. Murray, John W. Rice (1993)
A classic textbook
 Geometrical Foundations of Asymptotic Inference,
Robert E. Kass, Paul W. Vos (1997)
Geometrical Foundations of Asymptotic Inference,
Robert E. Kass, Paul W. Vos (1997)
A classic textbook
 Statistical decision rules and optimal inference,
N. N. Chentsov (1982)
Statistical decision rules and optimal inference,
N. N. Chentsov (1982)
The first textbook on information geometry, originally published in 1972 in Russian, and later translated in english by the AMS
 Information geometry: Near randomness and near independence,
Khadiga A. Arwini and Christopher T. J. Dodson (2008)
Information geometry: Near randomness and near independence,
Khadiga A. Arwini and Christopher T. J. Dodson (2008)
Books in Japanese

志摩裕彦, へッセ幾何学, 裳華房, 2001

入門 情報幾何: 統計的モデルをひもとく微分幾何学
Atsushi Fujioka (藤岡 敦著)
Kyoritsu publisher, 2021
Introduction to Information Geometry: Differential Geometry of Statistical Models

情報幾何学の基礎: 情報の内的構造を捉える新たな地平
Akio Fujiwara (藤原 彰夫)
Fundamentals of Information Geometry: A New Horizon for Capturing the Intrinsic Structure of Information
Kyoritsu publisher, 2021

情報幾何学の基礎 (数理情報科学シリーズ)
Akio Fujiwara (藤原 彰夫)
牧野書店 Makino bookstore.

情報幾何学の新展開 (SGCライブラリ)
Shun-ichi Amari (甘利 俊一)
Saiensu publisher, 2019.
A book compiling the columns which appeared in the
数理科学
(Mathematical sciences of Saiensu magazine)
-

情報幾何の方法, Shun-ichi Amari (甘利 俊一) and Hiroshi Nagaoka (長岡 浩司)
Iwanami press (1993, reprinted 2017)
-

情報理論, Shun-ichi Amari (甘利 俊一)
Information Theory
Chikuma Shobō (筑摩書房), 2011
Quantum information theory (QIT)/quantum information geometry (QIG)

Quantum Computation and Quantum Information
(10th Anniversary Edition) by Michael A. Nielsen, Isaac L. Chuang, Cambridge University Press, 2010

Quantum
Information Theory: Mathematical Foundation
by Masahito Hayashi, Springer, 2017
-

Quantum Riemannian Geometry
by Edwin J. Beggs , Shahn Majid, Springer, 2020
-

Geometry of Quantum States: An Introduction to Quantum Entanglement
by Ingemar Bengtsson and Karol Życzkowski, Cambridge University Press, 2009

Second edition
-

Quantum Information Theory and Quantum Statistics
by Dénes Petz, Springer, 2008
Other related books

Software/APIs
Category theory and information geometry
Since the seminal work of Chentsov who introduced the category of Markov kernels,
category theory plays an essential role in the very foundations of information geometry.
Below are some papers and links to explore this topic.
Home page of Evan Patterson
Home page of Geometric Science of Information
April 2022.
 The Many Faces of Information Geometry, AMS Notices (9 pages), 2022.
The Many Faces of Information Geometry, AMS Notices (9 pages), 2022.