Hilbert geometries for machine learning/AI

This is the home page for exploring the Hilbert geometry of the probability simplex in machine learning. We consider embeddings and clustering tasks. Hilbert geometries generalize the Klein and Cayley-Klein geometries by considering an open bounded convex domain Ω. The Hilbert distance can be extended to a projective distance on the cone C={(λ,λΩ) : λ∈R++}. The projective distance is also called Birkhoff cone distance.

Non-linear Embeddings in Hilbert Simplex Geometry

by Frank Nielsen and Ke Sun

Latest arXiv:2203.11434 report
Poster presented at ICML TAG-ML 2023
Slides
Python code zip file (for reproducible research, no warranties)

Graphical abstract:

@techrep{HSGEmbedding-2022,
  title={{Non-linear Embeddings in Hilbert Simplex Geometry}},
  author={Nielsen, Frank and Sun, Ke},
  number={2203.11434},
  institution={arXiv},
  note={Presented at ICML TAG-ML 2023}
  year={2022}
}

Clustering in Hilbert simplex geometry

by Frank Nielsen and Ke Sun
An invitation to machine learning in Hilbert geometries and Birkhoff projective geometries.

Latest paper revision
Chapter published in Geometric Structures of Information (Springer, 2019):
Clustering in Hilbert’s Projective Geometry: The Case Studies of the Probability Simplex and the Elliptope of Correlation Matrices.
Reproducible research:
- Python source code (for producing the figures and experiments of the paper)
- Java source code (experimentally check the information monotonicity Hilbert's simplex metric). Formal Proof
Hilbert balls in the simplex have hexagonal shapes On Balls in a Hilbert Polygonal Geometry (SoCG MM 2017 video)

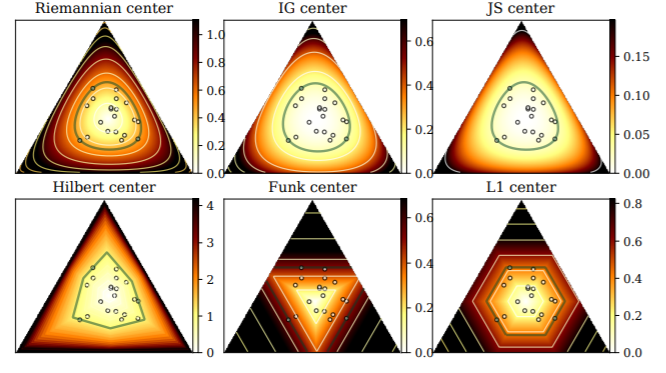
Visualizing the smallest enclosing ball in the probability simplex wrt to various distances:

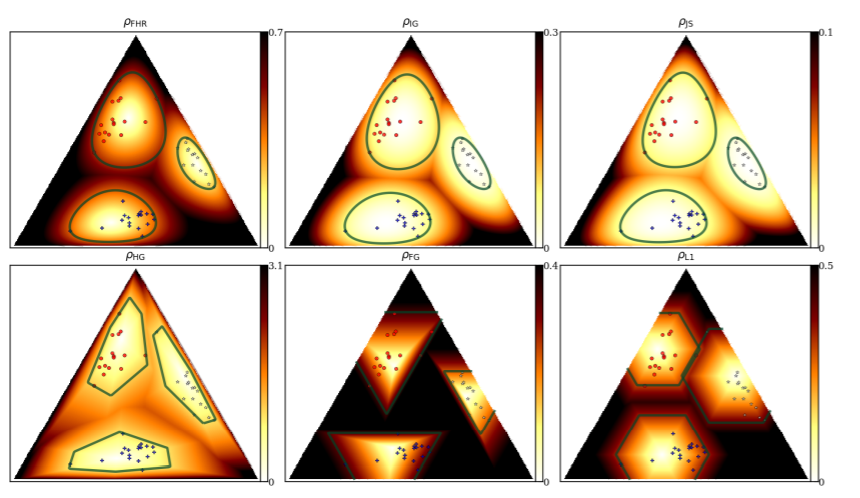
Visualizing a k-clustering:

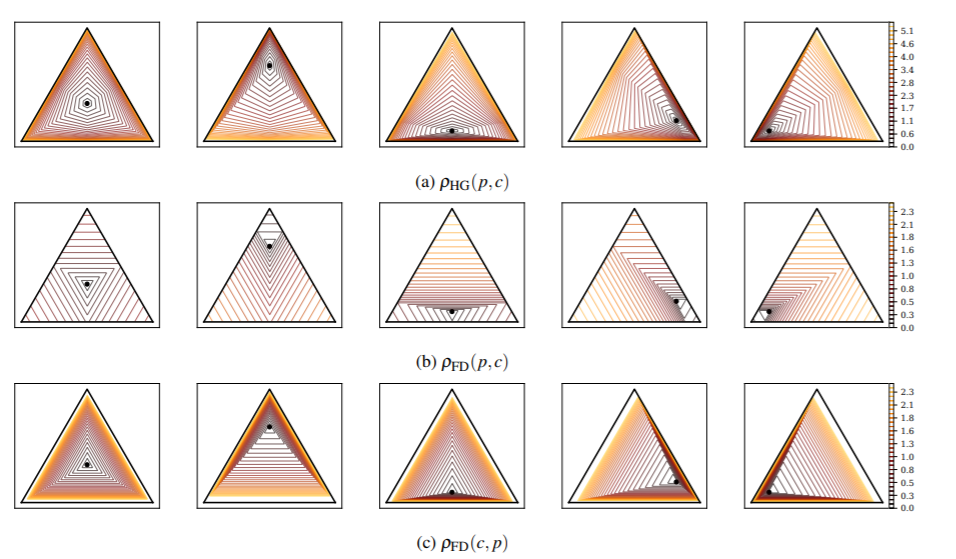
Visualizing forward and reverse Funk balls and Hilbert balls:

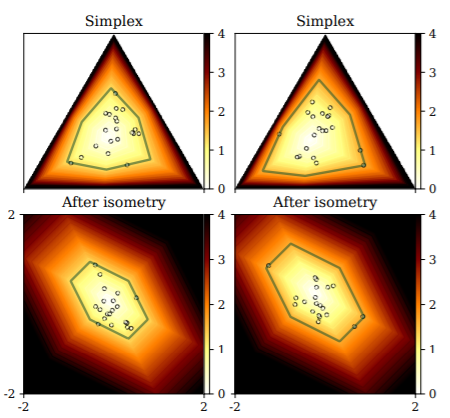
Visualizing a 1-clustering (minimax, smallest enclosing ball):

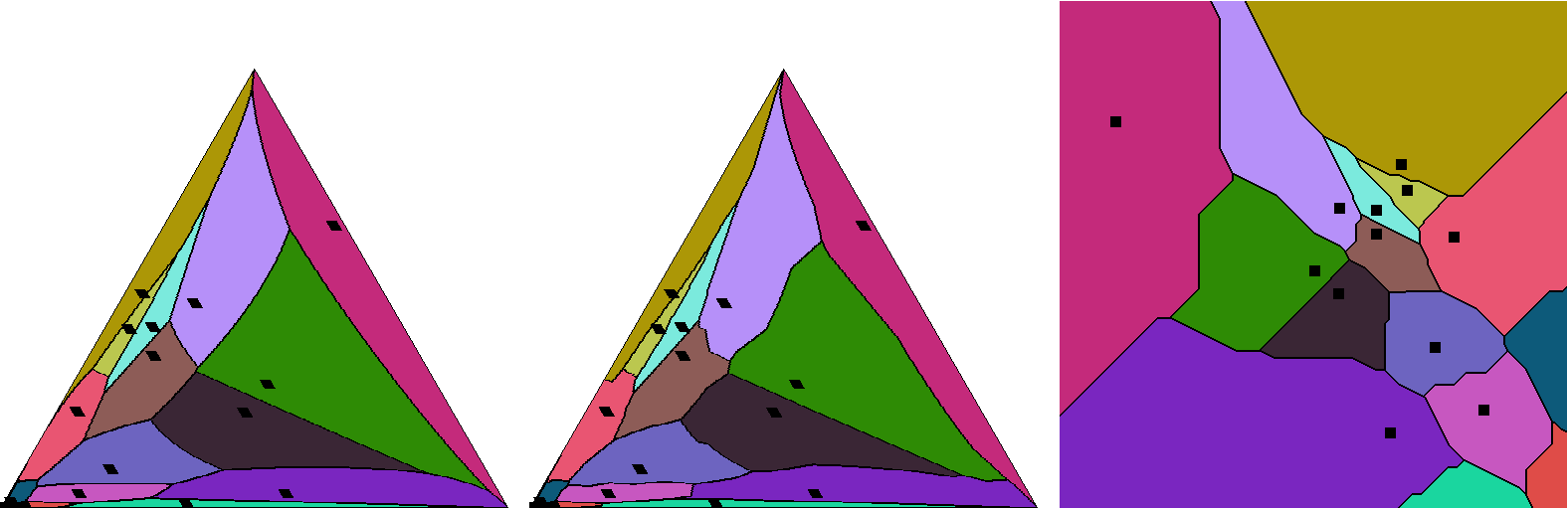
Voronoi diagrams with respect to the Aitchison distance (left), the Hilbert simplex distance (middle) and its equivalent variation norm space (right)

@incollection{HSEG-2019,
  title={{Clustering in Hilbert’s projective geometry: 
  The case studies of the probability simplex and the elliptope of correlation matrices}},
  author={Nielsen, Frank and Sun, Ke},
  booktitle={Geometric Structures of Information},
  pages={297--331},
  year={2019},
  publisher={Springer}
}	  
	  
@article{HSG-2017,
  title={{Clustering in Hilbert simplex geometry}},
  author={Nielsen, Frank and Sun, Ke},
  journal={arXiv preprint arXiv:1704.00454},
  year={2017}
}

@inproceedings{HSGball-2017,
  title={{On balls in a Hilbert polygonal geometry}},
  author={Nielsen, Frank and Shao, Laetitia},
  booktitle={33rd International Symposium on Computational Geometry (SoCG 2017)},
  year={2017},
  organization={Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik}
}

@techreport{CKML-2017,
  title={{Machine Learning with Cayley-Klein metrics}},
  author={Shao, La{\"e}titia and Nielsen, Frank},
  institution={Ecole Polytechnique},
  year={2017}
}

November 2018, last updated July 2023.