Consider the open cone ℝ₊₊^d of positive measures (i.e., histograms with d positive bins) with its open probability simplex subset Δ_d = {(x₁,…,x_d) ∈ ℝ₊^d  :  ∑ _i=1^dx_i = 1}. A point in Δ_d represents a multinoulli distribution (categorical distribution).

The f-divergence [1] between p,q ∈ Δ_d is defined for a convex function f(u) such that f(1) = 0 and f(u) strictly convex at 1 by:

For example, the Kullback-Leibler divergence is a f-divergence for f(u) = -log u.

All f-divergences are separable by construction: That is, they can be expressed as sum of coordinate-wise scalar divergences: Here, I_f[p : q] := ∑ _i=1^di_f(p[i] : q[i]), where i_f is a scalar f-divergence. Moreover, f-divergences are information monotone: That is, let 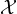= {X₁,…,X_m} be a partition of {1,…,n} into m ≤ n pairwise disjoint subsets X_i’s. For p ∈ Δ_n, let p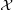_|∈ Δ_m denote the induced probability mass function with p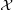_|[i] = ∑ _j∈Xip[i]. Then we have

Moreover, it can be shown that the only separable divergences satisfying this partition inequality are f-divergences [1] when n > 2. The special curious binary case n = 2 is dealt in [5].

Now, consider the non-separable Hilbert distance in the probability simplex [6]:

This dissimilarity measure is a projective distance on ℝ₊₊^d (Hilbert’s projective distance) because we have D_Hilbert[λp,λ′q] = D_Hilbert[p,q] for any λ,λ′ > 0. However, the Hilbert distance is a metric distance on Δ_d.

We state the main theorem:

Proof: We can represent the coarse-graining mapping pp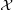_| by a linear application with a m × n matrix A with columns summing up to one (i.e., positive column-stochastic matrix):

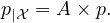
For example, the partition = {X₁ = {1,2},X₂ = {3,4}} (with n = 4 and m = 2) is represented by the matrix

Now, a key property of Hilbert distance is Birkhoff’s contraction mapping theorem [2, 3]:

where Δ(A) is called the projective diameter of the positive mapping A:

Since 0 ≤ tanh(x) ≤ 1 for x ≥ 0, we get the property that Hilbert distance on the probability simplex is an information monotone non-separable distance:

Notice that this holds for positive matrices and thus it includes the case of real matrix coefficients encoding deterministic Markov kernels. □

Another example of non-separable information monotone distance is Aitchison’s distance on the probability simplex [4] (using for compositional data analysis).

References