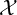 ,
,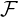 ,μ) be a measure space, and (w1,P1),…,(wn,Pn) be n weighted probability measures dominated
by a measure μ (with wi > 0 and ∑
wi = 1). Denote by
,μ) be a measure space, and (w1,P1),…,(wn,Pn) be n weighted probability measures dominated
by a measure μ (with wi > 0 and ∑
wi = 1). Denote by 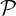 := {(w1,p1),…,(wn,pn)} the set of their
weighted Radon-Nikodym densities pi =
:= {(w1,p1),…,(wn,pn)} the set of their
weighted Radon-Nikodym densities pi = 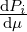 with respect to μ.
with respect to μ.
Lin coined the skewed Jensen-Shannon divergence between two distributions in 1991, and further extended it to the Jensen-Shannon diversity of a set of distributions. Sibson proposed the information radius based on Rényi α-entropies in 1969, and recovered for the special case of α = 1 the Jensen-Shannon diversity index. In this note, we summarize how the Jensen-Shannon divergence and diversity index were extended by either considering skewing vectors or using mixtures induced by generic means.
Let (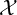 ,
,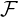 ,μ) be a measure space, and (w1,P1),…,(wn,Pn) be n weighted probability measures dominated
by a measure μ (with wi > 0 and ∑
wi = 1). Denote by
,μ) be a measure space, and (w1,P1),…,(wn,Pn) be n weighted probability measures dominated
by a measure μ (with wi > 0 and ∑
wi = 1). Denote by 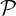 := {(w1,p1),…,(wn,pn)} the set of their
weighted Radon-Nikodym densities pi =
:= {(w1,p1),…,(wn,pn)} the set of their
weighted Radon-Nikodym densities pi = 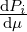 with respect to μ.
with respect to μ.
A statistical divergence D[p : q] is a measure of dissimilarity between two densities p and q (i.e., a
2-point distance) such that D[p : q] ≥ 0 with equality if and only if p(x) = q(x) μ-almost everywhere. A
statistical diversity index D(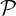 ) is a measure of variation of the weighted densities in
) is a measure of variation of the weighted densities in 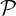 related to a
measure of centrality, i.e., a n-point distance which generalizes the notion of 2-point distance when
related to a
measure of centrality, i.e., a n-point distance which generalizes the notion of 2-point distance when
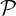 2(p,q) := {(
2(p,q) := {(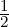 ,p1),(
,p1),(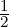 ,p2)}:
,p2)}:
![D [p : q] := D (P2(p,q)).](JensenShannonDiv3x.png)
The fundamental measure of dissimilarity in information theory is the I-divergence (also called the Kullback-Leibler divergence, KLD, see Equation (2.5) page 5 of [5]):
![∫ ( p(x))
DKL [p : q] := p(x)log ---- dμ(x).
X q(x)](JensenShannonDiv4x.png)
The KLD is asymmetric (hence the delimiter notation “:” instead of ‘,’) but can be symmetrized by defining the Jeffreys J-divergence (Jeffreys divergence, denoted by I2 in Equation (1) in 1946’s paper [4]):
![∫ (p(x))
DJ [p,q] := DKL [p : q]+ DKL [q : p] = (p(x) - q(x )) log q(x) dμ (x ).
X](JensenShannonDiv5x.png)
Although symmetric, any positive power of Jeffreys divergence fails to satisfy the triangle inequality: That is, DJα is never a metric distance for any α > 0, and furthermore DJα cannot be upper bounded.
In 1991, Lin proposed the asymmetric K-divergence (Equation (3.2) in [7]):
![[ ]
D [p : q] := D p : p-+-q ,
K KL 2](JensenShannonDiv6x.png)
and defined the L-divergence by analogy to Jeffreys’s symmetrization of the KLD (Equation (3.4) in [7]):
![DL [p,q] = DK [p : q]+ DK [q : p].](JensenShannonDiv7x.png)
By noticing that
![[ ]
p-+-q
DL [p,q] = 2h 2 - (h[p] + h[q]),](JensenShannonDiv8x.png)
where h denotes Shannon entropy (Equation (3.14) in [7]), Lin coined the (skewed) Jensen-Shannon divergence between two weighted densities (1 - α,p) and (α,q) for α ∈ (0,1) as follows (Equation (4.1) in [7]):
| (1) |
Finally, Lin defined the generalized Jensen-Shannon divergence (Equation (5.1) in [7]) for a finite weighted set of densities:
![[ ]
D [P] = h ∑ w p - ∑ w h[p ].
JS i i i i i i](JensenShannonDiv10x.png)
This generalized Jensen-Shannon divergence is nowadays called the Jensen-Shannon diversity index.
To contrast with the Jeffreys’ divergence, the Jensen-Shannon divergence (JSD) DJS := DJS,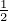 is upper
bounded by log 2 (does not require the densities to have the same support), and
is upper
bounded by log 2 (does not require the densities to have the same support), and 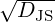 is a metric
distance [2, 3]. Lin cited precursor work [17, 8] yielding definition of the Jensen-Shannon divergence:
The Jensen-Shannon divergence of Eq. 1 is the so-called “increments of entropy” defined in (19) and (20)
of [17].
is a metric
distance [2, 3]. Lin cited precursor work [17, 8] yielding definition of the Jensen-Shannon divergence:
The Jensen-Shannon divergence of Eq. 1 is the so-called “increments of entropy” defined in (19) and (20)
of [17].
The Jensen-Shannon diversity index was also obtained very differently by Sibson in 1969 when he
defined the information radius [16] of order α using Rényi α-means and Rényi α-entropies [15]. In
particular, the information radius IR1 of order 1 of a weighted set 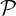 of densities is a diversity index
obtained by solving the following variational optimization problem:
of densities is a diversity index
obtained by solving the following variational optimization problem:
| (2) |
Sibson solved a more general optimization problem, and obtained the following expression (term K1 in Corollary 2.3 [16]):
![[ ]
IR [P] = h ∑ w p - ∑ w h[p ] := D [P].
1 i ii i i i JS](JensenShannonDiv14x.png)
Thus Eq. 2 is a variational definition of the Jensen-Shannon divergence.
The K-divergence of Lin can be skewed with a scalar parameter α ∈ (0,1) to give
| (3) |
Skewing parameter α was first studied in [6] (2001, see Table 2 of [6]). We proposed to unify the Jeffreys divergence with the Jensen-Shannon divergence as follows (Equation 19 in [9]):
| (4) |
When α = 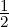 , we have DK,
, we have DK,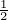 J = DJS, and when α = 1, we get DK,1J =
J = DJS, and when α = 1, we get DK,1J =  DJ.
DJ.
Notice that
![D α,β[p;q] := (1- β )D [p : (1- α )p + αq]+ βD [q : (1- α)p+ αq ]
JS KL KL](JensenShannonDiv20x.png)
amounts to calculate
![h×[(1- β )p + βq : (1- α )p+ αq ]- ((1 - β)h[p]+ βh[q])](JensenShannonDiv21x.png)
where
![∫
h ×[p,q] := - p(x) log q(x )d μ(x)](JensenShannonDiv22x.png)
denotes the cross-entropy. By choosing α = β, we have h×[(1-β)p+βq : (1-α)p+αq] = h[(1-α)p+αq], and thus recover the skewed Jensen-Shannon divergence of Eq. 1.
In [11] (2020), we considered a positive skewing vector α ∈ [0,1]k and a unit positive weight w belonging to the standard simplex Δk, and defined the following vector-skewed Jensen-Shannon divergence:
![k
D α,w[p : q] := ∑ DKL [(1- αi)p+ αiq : (1 - ¯α)p+ ¯αq], (5)
JS i=1
k
= h[(1- α¯)p+ ¯αq ]- ∑ h[(1 - α )p α q], (6)
i=1 i + i](JensenShannonDiv23x.png)
 [11].
[11].
![∑n ∑n
DJS [P ] = wiDKL [pi : ¯p] = h[¯p]- wih[pi].
i=1 i=1](JensenShannonDiv25x.png)
Unfortunately, the JSD between two Gaussian densities is not known in closed form because of the definite integral of a log-sum term (i.e., K-divergence between a density and a mixture density ). For the special case of the Cauchy family, a closed-form formula [14] for the JSD between two Cauchy densities was obtained. Thus we may choose a geometric mixture distribution [10] instead of the ordinary arithmetic mixture . More generally, we can choose any weighted mean Mα (say, the geometric mean, or the harmonic mean, or any other power mean) and define a generalization of the K-divergence of Equation 3:
| (7) |
where

is a statistical M-mixture with ZMα(p,q) denoting the normalizing coefficient:
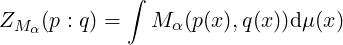
so that ∫ (pq)Mα(x)dμ(x) = 1. These M-mixtures are well-defined provided the convergence of the definite integrals.
Then we define a generalization of the JSD [10] termed (Mα,Nβ)-Jensen-Shannon divergence as follows:
| (8) |
where Nβ is yet another weighted mean to average the two Mα-K-divergences. We have
DJS = DJSA,A where A(a,b) = 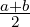 is the arithmetic mean. The geometric JSD yields a closed-form
formula between two multivariate Gaussians, and has been used in deep learning [1]. More
generally, we may consider the Jensen-Shannon symmetrization of an arbitrary distance D
as
is the arithmetic mean. The geometric JSD yields a closed-form
formula between two multivariate Gaussians, and has been used in deep learning [1]. More
generally, we may consider the Jensen-Shannon symmetrization of an arbitrary distance D
as
| (9) |
| (10) |
When Sw = Aw (with Aw(a1,…,an) = ∑ i=1nwiai the arithmetic weighted mean), we recover the ordinary Jensen-Shannon diversity index. More generally, we define the S-Jensen-Shannon index of an arbitrary distance D as
| (11) |
When n = 2, this yields a Jensen-Shannon-symmetrization of distance D.
The variational optimization defining the JSD can also be constrained to a (parametric) family of
densities  , thus defining the (S,
, thus defining the (S, )-relative Jensen-Shannon diversity index:
)-relative Jensen-Shannon diversity index:
| (12) |
The relative Jensen-Shannon divergences are useful for clustering applications: Let pθ1 and pθ2 be
two densities of an exponential family 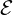 with cumulant function F(θ). Then the
with cumulant function F(θ). Then the 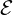 -relative
Jensen-Shannon divergence is the Bregman information of
-relative
Jensen-Shannon divergence is the Bregman information of 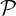 2(p,q) for the conjugate function
F*(η) = -h[pθ] (with η = ∇F(θ)). The
2(p,q) for the conjugate function
F*(η) = -h[pθ] (with η = ∇F(θ)). The 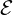 -relative JSD amounts to a Jensen divergence for
F*:
-relative JSD amounts to a Jensen divergence for
F*:
![1
DvJS [pθ1,pθ2] = min --{DKL [p θ1 : pθ]+ DKL [pθ2 : pθ]}, (13)
θ 2
= min 1-{BF [θ : θ1]+ BF [θ : θ2]}, (14)
θ 2
1- * *
= miηn 2 {BF [η1 : η]+ BF [η2 : η]}, (15)
F *(η1)+ F *(η2) * *
= -------2------- - F (η ), (16)
*
=: JF (η1,η2), (17)](JensenShannonDiv35x.png)
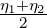 (a right-sided Bregman centroid [13]).
(a right-sided Bregman centroid [13]).
[1] Jacob Deasy, Nikola Simidjievski, and Pietro Liò. Constraining Variational Inference with Geometric Jensen-Shannon Divergence. In Advances in Neural Information Processing Systems, 2020.
[2] Dominik Maria Endres and Johannes E Schindelin. A new metric for probability distributions. IEEE Transactions on Information theory, 49(7):1858–1860, 2003.
[3] Bent Fuglede and Flemming Topsoe. Jensen-Shannon divergence and Hilbert space embedding. In International Symposium onInformation Theory, 2004. ISIT 2004. Proceedings., page 31. IEEE, 2004.
[4] Harold Jeffreys. An invariant form for the prior probability in estimation problems. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 186(1007):453–461, 1946.
[5] Solomon Kullback. Information theory and statistics. Courier Corporation, 1997.
[6] Lillian Lee. On the effectiveness of the skew divergence for statistical language analysis. In Artificial Intelligence and Statistics (AISTATS), page 65–72, 2001.
[7] Jianhua Lin. Divergence measures based on the Shannon entropy. IEEE Transactions on Information theory, 37(1):145–151, 1991.
[8] Jianhua Lin and SKM Wong. Approximation of discrete probability distributions based on a new divergence measure. Congressus Numerantium (Winnipeg), 61:75–80, 1988.
[9] Frank Nielsen. A family of statistical symmetric divergences based on Jensen’s inequality. arXiv preprint arXiv:1009.4004, 2010. URL https://arxiv.org/abs/1009.4004.
[10] Frank Nielsen. On the Jensen–Shannon Symmetrization of Distances Relying on Abstract Means. Entropy, 21(5), 2019. ISSN 1099-4300. doi: 10.3390/e21050485. URL https://www.mdpi.com/1099-4300/21/5/485.
[11] Frank Nielsen. On a Generalization of the Jensen–Shannon Divergence and the Jensen–Shannon Centroid. Entropy, 22(2), 2020. ISSN 1099-4300. doi: 10.3390/e22020221. URL https://www.mdpi.com/1099-4300/22/2/221.
[12] Frank Nielsen. On a Variational Definition for the Jensen-Shannon Symmetrization of Distances Based on the Information Radius. Entropy, 23(4), 2021. ISSN 1099-4300. doi: 10.3390/e23040464. URL https://www.mdpi.com/1099-4300/23/4/464.
[13] Frank Nielsen and Richard Nock. Sided and symmetrized Bregman centroids. IEEE transactions on Information Theory, 55(6):2882–2904, 2009.
[14] Frank Nielsen and Kazuki Okamura. On f-divergences between cauchy distributions. arXiv:2101.12459, 2021.
[15] Alfréd Rényi et al. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Contributions to the Theory of Statistics. The Regents of the University of California, 1961.
[16] Robin Sibson. Information radius. Zeitschrift für Wahrscheinlichkeitstheorie und verwandte Gebiete, 14(2):149–160, 1969.
[17] Andrew KC Wong and Manlai You. Entropy and distance of random graphs with application to structural pattern recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, (5):599–609, 1985.