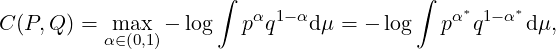To get a taste of computational information geometry (CIG), let us mention the following two
problems when implementing information-geometric structures and algorithms:
Thus computational information geometry aims at implementing robustly the information-geometric
structures and the geometric algorithms on those structures for various applications. To give two examples
of CIG, consider
[1] Shun-Ichi Amari. Natural gradient works efficiently in learning. Neural computation,
10(2):251–276, 1998.
[2] Shun-ichi Amari. Information geometry and its applications, volume 194. Springer, 2016.
[3] Shun-ichi Amari and Andrzej Cichocki. Information geometry of divergence functions.
Bulletin of the polish academy of sciences. Technical sciences, 58(1):183–195, 2010.
[4] Ovidiu Calin. Deep learning architectures. Springer, 2020.
[5] Herman Chernoff. A measure of asymptotic efficiency for tests of a hypothesis based on
the sum of observations. The Annals of Mathematical Statistics, pages 493–507, 1952.
[6] Frank Critchley and Paul Marriott. Computational information geometry in statistics:
theory and practice. Entropy, 16(5):2454–2471, 2014.
[7] Simon J Julier. An empirical study into the use of Chernoff information for robust,
distributed fusion of Gaussian mixture models. In 2006 9th International Conference on
Information Fusion, pages 1–8. IEEE, 2006.
[8] Wu Lin, Frank Nielsen, Khan Mohammad Emtiyaz, and Mark Schmidt. Tractable
structured natural-gradient descent using local parameterizations. In International Conference
on Machine Learning, pages 6680–6691. PMLR, 2021.
[9] James Martens. New insights and perspectives on the natural gradient method. Journal
of Machine Learning Research, 21(146):1–76, 2020.
[10] Naomichi Nakajima and Toru Ohmoto. The dually flat structure for singular models.
Information Geometry, 4(1):31–64, 2021.
[11] Frank Nielsen. An information-geometric characterization of Chernoff information. IEEE
Signal Processing Letters, 20(3):269–272, 2013.
[12] Frank Nielsen. Revisiting Chernoff information with likelihood ratio exponential families.
Entropy, 24(10):1400, 2022.
[13] Frank Nielsen, Frank Critchley, and Christopher TJ Dodson. Computational Information
Geometry. Springer, 2017.
[14] Frank Nielsen and GaŽtan Hadjeres. Monte carlo information-geometric structures.
Geometric Structures of Information, pages 69–103, 2019.
[15] Frank Nielsen and Richard Nock. On the smallest enclosing information disk. Information
Processing Letters, 105(3):93–97, 2008.
[16] Frank Nielsen and Alexander Soen. pyBregMan: A Python package for Bregman Manifolds.
Tokyo, Japan, 2024.
[17] Richard Nock and Frank Nielsen. Fitting the smallest enclosing Bregman ball. In European
Conference on Machine Learning, pages 649–656. Springer, 2005.
[18] Atsumi Ohara and Shinto Eguchi. Geometry on positive definite matrices deformed by
V -potentials and its submanifold structure. Geometric Theory of Information, pages 31–55,
2014.
[19] Hirohiko Shima. The geometry of Hessian structures. World Scientific, 2007.
[20] Ke Sun and Frank Nielsen. Relative Fisher information and natural gradient for learning
large modular models. In International Conference on Machine Learning, pages 3289–3298.
PMLR, 2017.
[21] Keiko Uohashi and Atsumi Ohara. Jordan algebras and dual affine connections on
symmetric cones. Positivity, 8:369–378, 2004.