Discrepancies, dissimilarities, divergences, and distances
Frank Nielsen
Sony Computer Science Laboratories Inc.
Tokyo, Japan
13th August 2021, updated August 16, 2021
This is a working document which will be frequently updated with materials concerning the
discrepancy between two distributions.
This document is also available in the PDF Distance.pdf
There are many other acronyms used in the literature for referencing a dissimilarity; For example, the
following 5 D’s: Discrepancies, deviations, dissimilarities, divergences, and distances.
Contents
1 Statistical distances between densities with computationally intractable normalizers
Consider a density p(x) = 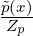 where
where  (x) is an unnormalized computable density and Zp = ∫
p(x)dμ(x)
the computationally intractable normalizer (also called in statistical physics the partition function or free
energy). A statistical distance D[p1 : p2] between two densities p1(x) =
(x) is an unnormalized computable density and Zp = ∫
p(x)dμ(x)
the computationally intractable normalizer (also called in statistical physics the partition function or free
energy). A statistical distance D[p1 : p2] between two densities p1(x) = 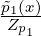 and p2(x) =
and p2(x) =  with
computationally intractable normalizers Zp1 and Zp2 is said projective (or two-sided homogeneous) if and
only if
with
computationally intractable normalizers Zp1 and Zp2 is said projective (or two-sided homogeneous) if and
only if
In particular, letting λ1 = Zp1 and λ2 = Zp2, we have
Notice that the rhs. does not rely on the computationally intractable normalizers. These projective
distances are useful in statistical inference based on minimum distance estimators [2] (see next
Section).
Here are a few statistical projective distances:
- γ-divergences (γ > 0) [10, 6]:
When γ → 0, we have [6] Dγ[p : q] = DKL[p : q], the Kullback-Leibler divergence (KLD).
For example, we can estimate the KLD between two densities of an exponential-polynomial
family by Monte Carlo stochastic integration of the γ-divergence for a small value of γ [27].
The γ-divergences (projective, Bregman-type=Cross-entropy-entropy) and the density power
divergence [1] (non-projective, Bregman-type divergence):
can be encapsulated into the family of Φ-power divergences [37] (functional density power
divergence class):
where ϕ(ex) convex and strictly increasing, ϕ continuous and twice continously differentiable
with finite second order derivatives. We have Dϕ,0[p : q] = ϕ′(1)∫
ℝp(x)log 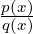 dμ(x) =
ϕ′(1)DKL[p : q].
dμ(x) =
ϕ′(1)DKL[p : q].
- Cauchy-Schwarz divergence [9] (CSD, projective)
and Hölder divergences [35] (HD, projective, which generalizes the CSD):
We have
and
Hölder divergences between two densities pθp and pθq of an exponential family with cumulant
function F(θ) is available in closed-form [35]:
The CSD is available in closed-form between mixtures of an exponential family with a conic
natural parameter [18]: This includes the case of Gaussian mixture models [11].
- Hilbert distance [34] (projective): Consider two probability mass functions p = (p1,…,pd)
and q = (q1,…,qd) of the d-dimensional probability simplex. Then the Hilbert distance is
We have
The Hilbert projective simplex distance can be extended to the cone of positive-definite
matrices [34] (and its subspace of correlation matrices called the elliptope) as follows:
where λmax(X) and λmin(X) denote the largest and smallest eigenvalue of matrix X,
respectively.
2 Statistical distances between empirical distributions and densities with computationally
intractable normalizers
When estimating the parameter 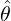 for a parametric family of distributions {pθ} from i.i.d. observations
for a parametric family of distributions {pθ} from i.i.d. observations
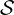 = {x1,…,xn}, we can define a minimum distance estimator (MDE):
= {x1,…,xn}, we can define a minimum distance estimator (MDE):
where p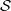 =
= 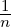 ∑
i=1nδxi is the empirical distribution (normalized). Thus we need only a right-sided
projective divergence to estimate models with computationally intractable normalizers. For example, the
Maximum Likelihood Estimator (MLE) is a MDE wrt. the KLD:
∑
i=1nδxi is the empirical distribution (normalized). Thus we need only a right-sided
projective divergence to estimate models with computationally intractable normalizers. For example, the
Maximum Likelihood Estimator (MLE) is a MDE wrt. the KLD:
It is thus interesting to study the impact of the choice of the distance D to the properties of the
corresponding estimator (e.g., γ-divergences yields provably robust estimators [6]).
3 The Jensen-Shannon divergence and some generalizations
3.1 Origins of the Jensen-Shannon divergence
Let (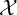 ,
,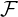 ,μ) be a measure space, and (w1,P1),…,(wn,Pn) be n weighted probability measures dominated
by a measure μ (with wi > 0 and ∑
wi = 1). Denote by
,μ) be a measure space, and (w1,P1),…,(wn,Pn) be n weighted probability measures dominated
by a measure μ (with wi > 0 and ∑
wi = 1). Denote by 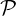 := {(w1,p1),…,(wn,pn)} the set of their
weighted Radon-Nikodym densities pi =
:= {(w1,p1),…,(wn,pn)} the set of their
weighted Radon-Nikodym densities pi = 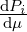 with respect to μ.
with respect to μ.
A statistical divergence D[p : q] is a measure of dissimilarity between two densities p and q (i.e., a
2-point distance) such that D[p : q] ≥ 0 with equality if and only if p(x) = q(x) μ-almost everywhere. A
statistical diversity index D(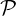 ) is a measure of variation of the weighted densities in
) is a measure of variation of the weighted densities in 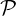 related to a
measure of centrality, i.e., a n-point distance which generalizes the notion of 2-point distance when
related to a
measure of centrality, i.e., a n-point distance which generalizes the notion of 2-point distance when
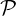 2(p,q) := {(
2(p,q) := {(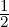 ,p1),(
,p1),(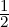 ,p2)}:
,p2)}:
The fundamental measure of dissimilarity in information theory is the I-divergence (also called the
Kullback-Leibler divergence, KLD, see Equation (2.5) page 5 of [12]):
The KLD is asymmetric (hence the delimiter notation “:” instead of ‘,’) but can be symmetrized by
defining the Jeffreys J-divergence (Jeffreys divergence, denoted by I2 in Equation (1) in 1946’s
paper [8]):
Although symmetric, any positive power of Jeffreys divergence fails to satisfy the triangle inequality:
That is, DJα is never a metric distance for any α > 0, and furthermore DJα cannot be upper
bounded.
In 1991, Lin proposed the asymmetric K-divergence (Equation (3.2) in [14]):
and defined the L-divergence by analogy to Jeffreys’s symmetrization of the KLD (Equation (3.4)
in [14]):
By noticing that
where h denotes Shannon entropy (Equation (3.14) in [14]), Lin coined the (skewed) Jensen-Shannon
divergence between two weighted densities (1 - α,p) and (α,q) for α ∈ (0,1) as follows (Equation (4.1)
in [14]):
Finally, Lin defined the generalized Jensen-Shannon divergence (Equation (5.1) in [14]) for a finite
weighted set of densities:
This generalized Jensen-Shannon divergence is nowadays called the Jensen-Shannon diversity
index.
To contrast with the Jeffreys’ divergence, the Jensen-Shannon divergence (JSD) DJS := DJS,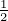 is upper
bounded by log 2 (does not require the densities to have the same support), and
is upper
bounded by log 2 (does not require the densities to have the same support), and  is a metric
distance [4, 5]. Lin cited precursor work [42, 15] yielding definition of the Jensen-Shannon divergence:
The Jensen-Shannon divergence of Eq. 1 is the so-called “increments of entropy” defined in (19) and (20)
of [42].
is a metric
distance [4, 5]. Lin cited precursor work [42, 15] yielding definition of the Jensen-Shannon divergence:
The Jensen-Shannon divergence of Eq. 1 is the so-called “increments of entropy” defined in (19) and (20)
of [42].
The Jensen-Shannon diversity index was also obtained very differently by Sibson in 1969 when he
defined the information radius [40] of order α using Rényi α-means and Rényi α-entropies [38]. In
particular, the information radius IR1 of order 1 of a weighted set 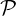 of densities is a diversity index
obtained by solving the following variational optimization problem:
of densities is a diversity index
obtained by solving the following variational optimization problem:
Sibson solved a more general optimization problem, and obtained the following expression (term K1 in
Corollary 2.3 [40]):
Thus Eq. 2 is a variational definition of the Jensen-Shannon divergence.
3.2 Some extensions of the Jensen-Shannon divergence
- Skewing the JSD.
The K-divergence of Lin can be skewed with a scalar parameter α ∈ (0,1) to give
Skewing parameter α was first studied in [13] (2001, see Table 2 of [13]). We proposed to unify
the Jeffreys divergence with the Jensen-Shannon divergence as follows (Equation 19
in [17]):
When α = 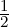 , we have DK,
, we have DK, J = DJS, and when α = 1, we get DK,1J =
J = DJS, and when α = 1, we get DK,1J = 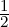 DJ.
DJ.
Notice that
amounts to calculate
where
denotes the cross-entropy. By choosing α = β, we have h×[(1-β)p+βq : (1-α)p+αq] = h[(1-α)p+αq],
and thus recover the skewed Jensen-Shannon divergence of Eq. 1.
In [21] (2020), we considered a positive skewing vector α ∈ [0,1]k and a unit positive weight w
belonging to the standard simplex Δk, and defined the following vector-skewed Jensen-Shannon
divergence:
where α = ∑
i=1kwiαi. The divergence DJSα,w generalizes the (scalar) skew Jensen-Shannon
divergence when k = 1, and is a Ali-Silvey-Csiszár f-divergence upper bounded by log  [21].
[21].
- A priori mid-density. The JSD can be interpreted as the total divergence of the densities to the
mid-density p = ∑
i=1nwipi, a statistical mixture:
Unfortunately, the JSD between two Gaussian densities is not known in closed form because of the
definite integral of a log-sum term (i.e., K-divergence between a density and a mixture density p).
For the special case of the Cauchy family, a closed-form formula [29] for the JSD between two
Cauchy densities was obtained. Thus we may choose a geometric mixture distribution [19] instead of
the ordinary arithmetic mixture p. More generally, we can choose any weighted mean Mα (say, the
geometric mean, or the harmonic mean, or any other power mean) and define a generalization of the
K-divergence of Equation 3:
where
is a statistical M-mixture with ZMα(p,q) denoting the normalizing coefficient:
so that ∫
(pq)Mα(x)dμ(x) = 1. These M-mixtures are well-defined provided the convergence of the
definite integrals.
Then we define a generalization of the JSD [19] termed (Mα,Nβ)-Jensen-Shannon divergence as
follows:
where Nβ is yet another weighted mean to average the two Mα-K-divergences. We have
DJS = DJSA,A where A(a,b) = 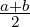 is the arithmetic mean. The geometric JSD yields a closed-form
formula between two multivariate Gaussians, and has been used in deep learning [3]. More
generally, we may consider the Jensen-Shannon symmetrization of an arbitrary distance D
as
is the arithmetic mean. The geometric JSD yields a closed-form
formula between two multivariate Gaussians, and has been used in deep learning [3]. More
generally, we may consider the Jensen-Shannon symmetrization of an arbitrary distance D
as
- A posteriori mid-density. We consider a generalization of Sibson’s information radius [40]. Let
Sw(a1,…,an) denote a generic weighted mean of n positive scalars a1,…,an, with weight
vector w ∈ Δn. Then we define the S-variational Jensen-Shannon diversity index [24]
as
When Sw = Aw (with Aw(a1,…,an) = ∑
i=1nwiai the arithmetic weighted mean), we recover the
ordinary Jensen-Shannon diversity index. More generally, we define the S-Jensen-Shannon index of
an arbitrary distance D as
When n = 2, this yields a Jensen-Shannon-symmetrization of distance D.
The variational optimization defining the JSD can also be constrained to a (parametric) family of
densities  , thus defining the (S,
, thus defining the (S, )-relative Jensen-Shannon diversity index:
)-relative Jensen-Shannon diversity index:
The relative Jensen-Shannon divergences are useful for clustering applications: Let pθ1 and pθ2 be
two densities of an exponential family  with cumulant function F(θ). Then the
with cumulant function F(θ). Then the  -relative
Jensen-Shannon divergence is the Bregman information of
-relative
Jensen-Shannon divergence is the Bregman information of  2(p,q) for the conjugate function
F*(η) = -h[pθ] (with η = ∇F(θ)). The
2(p,q) for the conjugate function
F*(η) = -h[pθ] (with η = ∇F(θ)). The 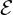 -relative JSD amounts to a Jensen divergence for
F*:
-relative JSD amounts to a Jensen divergence for
F*:
since η* := 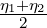 (a right-sided Bregman centroid [26]).
(a right-sided Bregman centroid [26]).
4 Statistical distances between mixtures
Pearson [36] first considered a unimodal Gaussian mixture of two components for modeling distributions
crabs in 1894. Statistical mixtures [16] like the Gaussian mixture models (GMMs) are often
met in information sciences, and therefore it is important to assess their dissimilarities. Let
m(x) = ∑
i=1kwipi(x) and m′(x) = ∑
i=1k′wi′pi′(x) be two finite statistical mixtures. The KLD between
two GMMs m and m′ is not analytic [41] because of the log-sum terms:
However, the KLD between two GMMs with the same prescribed components pi(x) = pi′(x) = pμi,Σi(x)
(i.e., k = k′, and only the normalized positive weights may differ) is provably a Bregman divergence [28]
for the differential negentropy F(θ):
where m(θ) = ∑
i=1k-1wipi(x) + (1 -∑
i=1k-1wi)pk(x) and F(θ) = ∫
m(θ)log m(θ)dx. The family
{mθ θ ∈ Δk-1∘} is called a mixture family in information geometry, where Δk-1∘ denotes the
(k - 1)-dimensional open standard simplex. However, F(θ) is usually not available in closed-form
because of the log-sum integral. In some special cases like the mixture of two prescribed Cauchy
distributions, we get a closed-form formula for the KLD, JSD, etc. [30, 25]. Thus when dealing
with mixtures (like GMMs), we either need efficient approximating (§4.1), bounding (§4.2)
KLD techniques, or new distances (§4.3) that yields closed-form formula between mixture
densities.
4.1 Approximating and/or fast statistical distances between mixtures
- The Jeffreys divergence (JD) DJ[m,m′] = DKL[m : m′]+DKL[m′ : m] between two (Gaussian)
MMs is not available in closed-form, and can be estimated using Monte Carlo integration as
where 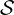 s = {x1,…,xs} are s IID samples from the mid mixture m12(x) :=
s = {x1,…,xs} are s IID samples from the mid mixture m12(x) := 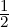 (m(x) + m′(x))
(with lims→∞
(m(x) + m′(x))
(with lims→∞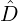 J
J s[m,m′] = DJ[m,m′]). In [23], the mixtures m and m′ are converted into
densities of an exponential-polynomial family. The JD between densities pθ and pθ′ of an
exponential family with cumulant function F is available in closed-form:
s[m,m′] = DJ[m,m′]). In [23], the mixtures m and m′ are converted into
densities of an exponential-polynomial family. The JD between densities pθ and pθ′ of an
exponential family with cumulant function F is available in closed-form:
with η = ∇F(θ) and θ = ∇F*(η), where F* denotes the convex conjugate. Any smooth
density r (includes a mixture r = m) is converted into close densities pθrMLE and pηrSME
of a exponential-polynomial family using extensions of the Maximum Likelihood Estimator
(MLE) and Score Matching Estimator (SME). Then JD between mixtures is approximated
as follows
- Given a finite set of mixtures {mi(x)} sharing the same components (e.g., points on a
mixture family manifold), we precompute the KLD between pairwise components to obtain
fast approximation of the KLD DKL[mi : mj] between any two mixtures mi and mj, see [39].
4.2 Bounding statistical distances between mixtures
- Log-Sum-Exp bounds: In [31, 32], we lower and upper bound the cross-entropy between
mixtures using the fact that the log-sum term log m(x) and be interpreted as a LSE function.
We then compute lower envelopes and upper envelopes of density functions using technique
of computational geometry to report deterministic lower and upper bounds on the KLD and
α-divergences. These bounds are said combinatorial because we decompose the support into
elementary intervals. Bounds between the Total Variation Distance (TVD) between univariate
mixtures are reported in [33].
4.3 Newly designed statistical distances yielding closed-form formula for mixtures
- Statistical Minkowski distances [20]: Consider the Lebesgue space
for α ≥ 1, where F denotes the set of all real-valued measurable functions defined on the support  .
Minkowski’s inequality writes as ∥p + q∥α ≤∥p∥α + ∥q∥α for α ∈ [1,∞). The statistical Minkowski
difference distance between p,q ∈ Lα(μ) is defined as
.
Minkowski’s inequality writes as ∥p + q∥α ≤∥p∥α + ∥q∥α for α ∈ [1,∞). The statistical Minkowski
difference distance between p,q ∈ Lα(μ) is defined as
The statistical Minkowski log-ratio distance is defined by:
These statistical Minkowski distances are symmetric, and Lα[p,q] is scale-invariant. For even
integers α ≥ 2, DαMinkowski[m : m′] is available in closed-form.
- We show that the Cauchy-Schwarz divergence (CSD), the quadratic Jensen-Rényi divergence (JRD),
and the total square Distance (TSD) between two GMMs, and more generally two mixtures of
exponential families, can be obtained in closed-form in [18].
Initially created 13th August 2021 (last updated August 16, 2021).
References
[1] Ayanendranath Basu, Ian R Harris, Nils L Hjort, and MC Jones. Robust and efficient
estimation by minimising a density power divergence. Biometrika, 85(3):549–559, 1998.
[2] Ayanendranath Basu, Hiroyuki Shioya, and Chanseok Park. Statistical inference: the
minimum distance approach. Chapman and Hall/CRC, 2019.
[3] Jacob Deasy, Nikola Simidjievski, and Pietro Liò. Constraining Variational Inference
with Geometric Jensen-Shannon Divergence. In Advances in Neural Information Processing
Systems, 2020.
[4] Dominik Maria Endres and Johannes E Schindelin. A new metric for probability
distributions. IEEE Transactions on Information theory, 49(7):1858–1860, 2003.
[5] Bent Fuglede and Flemming Topsoe. Jensen-Shannon divergence and Hilbert space
embedding. In International Symposium onInformation Theory, 2004. ISIT 2004. Proceedings.,
page 31. IEEE, 2004.
[6] Hironori Fujisawa and Shinto Eguchi. Robust parameter estimation with a small bias
against heavy contamination. Journal of Multivariate Analysis, 99(9):2053–2081, 2008.
[7] Aapo Hyvärinen and Peter Dayan. Estimation of non-normalized statistical models by
score matching. Journal of Machine Learning Research, 6(4), 2005.
[8] Harold Jeffreys. An invariant form for the prior probability in estimation problems.
Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences,
186(1007):453–461, 1946.
[9] Robert Jenssen, Jose C Principe, Deniz Erdogmus, and Torbjørn Eltoft. The
Cauchy–Schwarz divergence and Parzen windowing: Connections to graph theory and Mercer
kernels. Journal of the Franklin Institute, 343(6):614–629, 2006.
[10] MC Jones, Nils Lid Hjort, Ian R Harris, and Ayanendranath Basu. A comparison of
related density-based minimum divergence estimators. Biometrika, 88(3):865–873, 2001.
[11] Kittipat Kampa, Erion Hasanbelliu, and Jose C Principe. Closed-form Cauchy-Schwarz
PDF divergence for mixture of Gaussians. In The 2011 International Joint Conference on
Neural Networks, pages 2578–2585. IEEE, 2011.
[12] Solomon Kullback. Information theory and statistics. Courier Corporation, 1997.
[13] Lillian Lee. On the effectiveness of the skew divergence for statistical language analysis.
In Artificial Intelligence and Statistics (AISTATS), page 65?72, 2001.
[14] Jianhua Lin. Divergence measures based on the Shannon entropy. IEEE Transactions on
Information theory, 37(1):145–151, 1991.
[15] Jianhua Lin and SKM Wong. Approximation of discrete probability distributions based
on a new divergence measure. Congressus Numerantium (Winnipeg), 61:75–80, 1988.
[16] Geoffrey J McLachlan and Kaye E Basford. Mixture models: Inference and applications
to clustering, volume 38. M. Dekker New York, 1988.
[17] Frank Nielsen. A family of statistical symmetric divergences based on Jensen’s inequality.
arXiv preprint arXiv:1009.4004, 2010.
[18] Frank Nielsen. Closed-form information-theoretic divergences for statistical mixtures.
In Proceedings of the 21st International Conference on Pattern Recognition (ICPR), pages
1723–1726. IEEE, 2012.
[19] Frank Nielsen. On the Jensen?Shannon Symmetrization of Distances Relying on Abstract
Means. Entropy, 21(5), 2019.
[20] Frank Nielsen. The statistical Minkowski distances: Closed-form formula for Gaussian
mixture models. In International Conference on Geometric Science of Information, pages
359–367. Springer, 2019.
[21] Frank Nielsen. On a Generalization of the Jensen?Shannon Divergence and the
Jensen?Shannon Centroid. Entropy, 22(2), 2020.
[22] Frank Nielsen. Fast approximations of the Jeffreys divergence between univariate Gaussian
mixture models via exponential polynomial densities. arXiv preprint arXiv:2107.05901, 2021.
[23] Frank Nielsen. Fast approximations of the jeffreys divergence between univariate gaussian
mixture models via exponential polynomial densities. arXiv preprint arXiv:2107.05901, 2021.
[24] Frank Nielsen. On a Variational Definition for the Jensen-Shannon Symmetrization of
Distances Based on the Information Radius. Entropy, 23(4), 2021.
[25] Frank Nielsen. The dually flat information geometry of the mixture family of two prescribed
Cauchy components. arXiv preprint arXiv:2104.13801, 2021.
[26] Frank Nielsen and Richard Nock. Sided and symmetrized Bregman centroids. IEEE
transactions on Information Theory, 55(6):2882–2904, 2009.
[27] Frank Nielsen and Richard Nock. Patch matching with polynomial exponential families
and projective divergences. In International Conference on Similarity Search and Applications,
pages 109–116. Springer, 2016.
[28] Frank Nielsen and Richard Nock. On the geometry of mixtures of prescribed distributions.
In IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pages
2861–2865. IEEE, 2018.
[29] Frank Nielsen and Kazuki Okamura. On f-divergences between cauchy distributions.
arXiv:2101.12459, 2021.
[30] Frank Nielsen and Kazuki Okamura. On f-divergences between Cauchy distributions.
arXiv preprint arXiv:2101.12459, 2021.
[31] Frank Nielsen and Ke Sun. Guaranteed bounds on information-theoretic measures of
univariate mixtures using piecewise log-sum-exp inequalities. Entropy, 18(12):442, 2016.
[32] Frank Nielsen and Ke Sun. Combinatorial bounds on the α-divergence of univariate
mixture models. In 2017 IEEE International Conference on Acoustics, Speech and Signal
Processing, ICASSP 2017, New Orleans, LA, USA, March 5-9, 2017, pages 4476–4480. IEEE,
2017.
[33] Frank Nielsen and Ke Sun. Guaranteed Deterministic Bounds on the total variation
distance between univariate mixtures. In 28th IEEE International Workshop on Machine
Learning for Signal Processing, MLSP 2018, Aalborg, Denmark, September 17-20, 2018, pages
1–6. IEEE, 2018.
[34] Frank Nielsen and Ke Sun. Clustering in Hilbert’s projective geometry: The case studies
of the probability simplex and the elliptope of correlation matrices. In Geometric Structures
of Information, pages 297–331. Springer, 2019.
[35] Frank Nielsen, Ke Sun, and Stéphane Marchand-Maillet. On Hölder projective
divergences. Entropy, 19(3):122, 2017.
[36] Karl Pearson. Contributions to the mathematical theory of evolution. Philosophical
Transactions of the Royal Society of London. A, 185:71–110, 1894.
[37] Souvik Ray, Subrata Pal, Sumit Kumar Kar, and Ayanendranath Basu. Characterizing
the functional density power divergence class. arXiv preprint arXiv:2105.06094, 2021.
[38] Alfréd Rényi et al. On measures of entropy and information. In Proceedings of the Fourth
Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Contributions to
the Theory of Statistics. The Regents of the University of California, 1961.
[39] Olivier Schwander, Stéphane Marchand-Maillet, and Frank Nielsen. Comix: Joint
estimation and lightspeed comparison of mixture models. In 2016 IEEE International
Conference on Acoustics, Speech and Signal Processing, ICASSP 2016, Shanghai, China,
March 20-25, 2016, pages 2449–2453. IEEE, 2016.
[40] Robin Sibson. Information radius. Zeitschrift für Wahrscheinlichkeitstheorie und verwandte
Gebiete, 14(2):149–160, 1969.
[41] Sumio Watanabe, Keisuke Yamazaki, and Miki Aoyagi. Kullback information of normal
mixture is not an analytic function. IEICE technical report. Neurocomputing, 104(225):41–46,
2004.
[42] Andrew KC Wong and Manlai You. Entropy and distance of random graphs with
application to structural pattern recognition. IEEE Transactions on Pattern Analysis and
Machine Intelligence, (5):599–609, 1985.
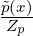 where
where  (x) is an unnormalized computable density and Zp = ∫
p(x)dμ(x)
the computationally intractable normalizer (also called in statistical physics the partition function or free
energy). A statistical distance D[p1 : p2] between two densities p1(x) =
(x) is an unnormalized computable density and Zp = ∫
p(x)dμ(x)
the computationally intractable normalizer (also called in statistical physics the partition function or free
energy). A statistical distance D[p1 : p2] between two densities p1(x) = 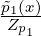 and p2(x) =
and p2(x) =  with
computationally intractable normalizers Zp1 and Zp2 is said projective (or two-sided homogeneous) if and
only if
with
computationally intractable normalizers Zp1 and Zp2 is said projective (or two-sided homogeneous) if and
only if
![∀λ1 > 0,λ2 > 0, D[p1 : p2] = D [λ1p1 : λ2p2].](Distance4x.png)
![D [p : p ] = D[˜p : ˜p ].
1 2 1 2](Distance5x.png)
![(∫ ) ( ) ( ∫ ) (∫ )
D γ[p : q] := log qα+1 - 1+ 1- log qαp + 1-log pα+1 , γ ≥ 0
ℝ α ℝ α ℝ](Distance6x.png)
![∫ ( ) ∫ ∫
dpd α+1 1- α 1- α+1
D α [p : q] := ℝq - 1+ α ℝ q p+ α ℝp , α ≥ 0,](Distance7x.png)
![( ∫ ) ( 1 ) ( ∫ ) 1 ( ∫ )
D ϕ,α[p : q] := ϕ qα+1 - 1 + -- ϕ qαp + -ϕ pα+1 , α ≥ 0,
ℝ α ℝ α ℝ](Distance8x.png)
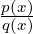 d
d![( )
∫
DCS[p : q] = - log( ∘-∫---p(x-)q(x)∫dμ-(x)-----) = DCS [λ1p : λ2q],∀λ1 > 0,λ2 > 0,
p(x)2dμ(x) q(x)2dμ(x)](Distance10x.png)
![( ∫ γ∕α γ∕β )
DH ¨older[p : q] = - log-------X-p(x-)--q(x)---dx------ , 1-+ 1-= 1.
α,γ (∫ p(x)γdx)1∕α(∫ q(x)γdx)1∕β α β
X X](Distance11x.png)
![H ¨older H ¨older
∀ λ1 > 0,λ2 > 0,D α,γ [λ1p : λ2q] = D α,γ [p : q],](Distance12x.png)
![DH2¨o,2lder[p : q] = DCS [p : q].](Distance13x.png)
![1 1 ( γ γ )
DHα,¨oγlder[p : q] =-F (γθp)+ --F (γθq)- F -θp + -θq
α β α β](Distance14x.png)
![( pi)
Hilbert maxi-∈{1,...,d}-qi
D [p : q] = log minj ∈{1,...,d} pj .
qj](Distance15x.png)
![Hilbert Hilbert
∀λ1 > 0,λ2 > 0,D [λ1p : λ2q] = D [p : q].](Distance16x.png)
![( - 1)
DHilbert[P : Q ] = log λmax(P-Q-)- ,
λmin(PQ -1)](Distance17x.png)
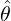 for a parametric family of distributions
for a parametric family of distributions 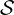
![θˆ= argmin D [pS : pθ],
θ](Distance19x.png)
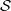
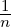
![θˆMLE = argmin DKL [pS : pθ].
θ](Distance21x.png)
![∫
DHyv ¨arinen [p : pθ] := 1 ∥∇x logp(x) - ∇x log pθ(x)∥2 p(x)dx.
2](Distance22x.png)
![∫
DHyv ¨arinen[p : q] := 1 p(x )α (∇ log p(x)- ∇ logq(x))2dx, α > 0.
α 2 x x](Distance23x.png)
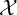
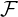
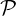
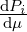 with respect to
with respect to 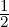
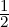
![D [p : q] := D (P2(p,q)).](Distance27x.png)
![∫ ( p(x))
DKL [p : q] := p(x)log q(x) dμ(x).
X](Distance28x.png)
![∫ ( )
DJ [p,q] := DKL [p : q]+ DKL [q : p] = (p(x) - q(x )) log p(x) d μ(x).
X q(x)](Distance29x.png)
![[ ]
DK [p : q] := DKL p : p-+-q ,
2](Distance30x.png)
![DL [p,q] = DK [p : q]+ DK [q : p].](Distance31x.png)
![[ ]
p-+-q
DL [p,q] = 2h 2 - (h[p]+ h[q]),](Distance32x.png)
![DJS,α[p,q] = h[(1- α)p + αq]- (1 - α)h[p]- αh[q].](Distance33x.png)
![[ ]
∑ ∑
DJS [P ] = h wipi - wih [pi].
i i](Distance34x.png)
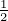 is upper
bounded by log 2 (does not require the densities to have the same support), and
is upper
bounded by log 2 (does not require the densities to have the same support), and  is a metric
distance
is a metric
distance ![n
IR [P ] := min ∑ w D [p : c].
1 c i KL i
i=1](Distance37x.png)
![[ ]
∑ ∑
IR1 [P ] = h wipi - wih [pi] := DJS[P ].
i i](Distance38x.png)
![DK, α[p : q] := DKL [p : (1- α )p+ αq].](Distance39x.png)
![DJ [p : q] := DK,α-[p-: q]+-DK,-α[q-: p].
K,α 2](Distance40x.png)
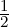 , we have
, we have 
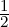
![α,β
D JS [p;q] := (1- β )DKL [p : (1- α )p + αq]+ βDKL [q : (1- α)p+ αq ]](Distance44x.png)
![h×[(1- β )p + βq : (1- α )p+ αq ]- ((1 - β)h[p]+ βh[q])](Distance45x.png)
![∫
×
h [p,q] := - p (x )log q(x)dμ(x)](Distance46x.png)
![∑k
DαJ,Sw[p : q] := DKL [(1 - αi)p+ αiq : (1 - ¯α)p + ¯αq], (5)
i=1
∑k
= h[(1- α¯)p + ¯αq]- h[(1- αi)p+αiq], (6)
i=1](Distance47x.png)

![∑n ∑n
DJS [P ] = wiDKL [pi : ¯p] = h[¯p]- wih [pi].
i=1 i=1](Distance49x.png)
![DM α [p : q] := D [p : (pq) ],
K K M α](Distance50x.png)

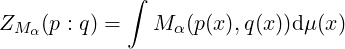
![Mα,Nβ
D JS [p : q ] := N β (DK [p : (pq)Mα],DK [q : (pq)M α]) ,](Distance53x.png)
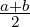 is the arithmetic mean. The geometric JSD yields a closed-form
formula between two multivariate Gaussians, and has been used in deep learning
is the arithmetic mean. The geometric JSD yields a closed-form
formula between two multivariate Gaussians, and has been used in deep learning ![DJMS ,N [p : q] := N β (D [p : (pq)Mα],D [q : (pq)Mα]).
α β](Distance55x.png)
![DSw (P ) := min Sw (DKL [p1 : c],DKL [pn : c]) .
vJS c](Distance56x.png)
![DvJS (P) := minSw (D [p1 : c],...,D [pn : c]).
Sw c](Distance57x.png)

![DSw,D (P ) := min Sw (DKL [p1 : c],...,DKL [pn : c]).
vJS c∈D](Distance58x.png)
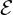
![DvJS [p ,p ] = min 1-{DKL [p : p ]+ DKL [p : p ]}, (13)
θ1 θ2 θ 2 θ1 θ θ2 θ
1-
= miθn 2 {BF [θ : θ1]+ BF [θ : θ2]}, (14)
1
= miηn 2-{BF *[η1 : η]+ BF *[η2 : η]}, (15)
* *
= F--(η1)+-F--(η2) - F*(η*), (16)
2
=: JF *(η1,η2), (17)](Distance59x.png)
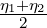 (a right-sided
(a right-sided ![∫
′ m-(x)-
DKL [m : m ] = m (x)log m ′(x)dx.](Distance61x.png)
![DKL [m (θ) : m (θ′)] = BF (θ,θ′),](Distance62x.png)
![( )
ˆSs ′ 1∑s (m(xi)--m-′(xi))- m-(xi)-
D J [m, m ] := s 2 m(xi)+ m ′(xi) log m′(xi) ,
i=1](Distance63x.png)
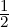 (
(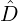
![′ ′
DJ[pθ,pθ′] = (θ - θ)⋅(η - η),](Distance66x.png)
![′ ′SME SME ′MLE MLE
DJ [m, m ] ≃ (θ - θ ) ⋅(η - η ).](Distance67x.png)
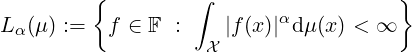
![DMinkowski[p,q] := ∥p∥α + ∥q∥α - ∥p+ q∥α ≥ 0.
α](Distance69x.png)
![LMinkowski[p,q] := - log -∥p-+-q∥α--≥ 0.
α ∥p∥α + ∥q∥ α](Distance70x.png)