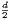This column is also available in pdf: filename AdaptiveAlgorithmKleeMeasure.pdf

In 1977, Klee [4] asked whether the union ∪_i=1ⁿ[a_i,b_i] of a set of n intervals can be computed in less than O(nlog n) or not. In general, the Klee’s measure problem (KMP) asks to calculate the union ∪_i=1ⁿB_i of n axis-parallel boxes (also called isothetic boxes) in ℝ^d. This problem can be solved deterministically in O(nlog n) time for d ∈{1,2}, and (so far) in O(n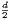^⌈⌉) for arbitrary d ≥ 3, see Chan [3] (2013).

A simple Monte Carlo algorithm [2] consists in sampling uniformly s points (iid) in the smallest axis-parallel bounding box B of ∪_i=1ⁿB_i: The probability of a sample point to fall inside the union U = ∪_i=1ⁿB_i is 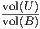. Therefore vol(U) ≃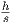vol(B), where h denote the number of points falling in U. This is a probabilistic algorithm that runs in Õ(nsd) time.

Getting back to Klee’s original question: Can we beat the O(nlog n) bound (even in 1D)? This is where two computational aspects pop up: (1) the model of computation, and (2) the concept of adaptive parameter:

1. It is common to consider the real RAM (random access machine) model of computation where arithmetic operations are carried in constant time on real numbers (without any precision limitations). If instead, we consider the word RAM model [3] (integer input coded using w bits), KMP can be solved in O.
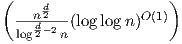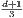2. For special input cases like hypercubes or fat boxes [3], KMP can be solved faster: For example, in O(n log ^O(1)n) for hypercubes. The 1D (interval) KMP can be solved in O(nlog p) where p denotes the number of piercing points to stab¹ all intervals [8]. Clearly, p is an adaptive parameter that depends on the input configuration. So even, if we fix a computation model, there are potentially many adaptive parameters to consider to improve the computational complexity. So a modern extension of Klee’s measure problem is to ask whether we can beat the O(nlog p) bound (on real RAM)? Let c denote the number of connected components of U = ∪_i=1ⁿ[a_i,b_i]. Is it possible to get a O(nlog c) bound. Well, when p = 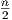and c = 1, we need O(nlog n) time to detect that we have a single component in the union. Indeed, consider the MaxGap problem that consists in finding the largest gap Δ between two consecutive scalars in a given set {x₁,…,x_n}. Consider the set of intervals {B_i = [x_i,x_i + δ]}_i. Then ∪_i=1ⁿB_i has a single component if and only if δ ≥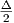. On the real RAM model of computation, MaxGap has lower bound Ω(nlog n) (see [9], p. 261). However, by using the floor function and the pigeon principle, one can get a simple linear time algorithm for MaxGap.

   It is not easy to find adaptive (computational) parameters. For example, consider computing the diameter [5] of a set of n points of ℝ². Solving this problem requires Ω(nlog n)-time on the algebraic computation-tree model. However, we can compute the smallest enclosing disk in Θ(n) time [6]: When a pair of antipodal points are on the border of the smallest enclosing disk, it defines the diameter.

   In general, adaptive algorithms refine the concept of output-sensitive algorithms by allowing one to take into account further attributes of the input configuration that can be used to improve the overall running time [7] (1996). See also the instance-optimal geometric algorithms [1] (2017).

References