 (d) denote the set of multivariate
normal distributions:
(d) denote the set of multivariate
normal distributions:
Let ℙ(d) denote the set of symmetric positive?definite (SPD) d×d matrices and  (d) denote the set of multivariate
normal distributions:
(d) denote the set of multivariate
normal distributions:

The Fisher-Rao distance between two normals N(μ1,Σ1) and N(μ2,Σ2) is the geodesic Riemannian distance on
the manifold ( ,gFisher) induced by the Fisher information metric:
,gFisher) induced by the Fisher information metric:
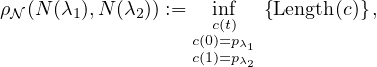
where
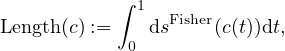
and dsFisher(t) := 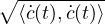 c(t) is the Fisher-Rao length element. The inner product ⟨v1,v2⟩N for
v1,v2 ∈ TN
c(t) is the Fisher-Rao length element. The inner product ⟨v1,v2⟩N for
v1,v2 ∈ TN at normal N is the called the Fisher-Rao norm (with tangent planes TN
at normal N is the called the Fisher-Rao norm (with tangent planes TN is identified to
ℝd × Sym(d) where Sym(d) be the set of d × d symmetric matrices). The statistical model
is identified to
ℝd × Sym(d) where Sym(d) be the set of d × d symmetric matrices). The statistical model  (d) is of dimension
m = dim(Λ(d)) = d +
(d) is of dimension
m = dim(Λ(d)) = d + 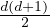 =
= 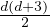 and identifiable: there is a one-to-one correspondence λ ↔ pλ(x) between
λ ∈ Λ(d) and N(μ,Σ) ∈
and identifiable: there is a one-to-one correspondence λ ↔ pλ(x) between
λ ∈ Λ(d) and N(μ,Σ) ∈ (d).
(d).
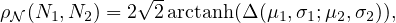
where Δ(a,b;c,d) = 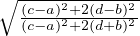 is a Möbius distance and arctanh(u) :=
is a Möbius distance and arctanh(u) := 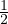 log
log  for
0 ≤ u < 1. The Fisher-Rao geodesics are semi-ellipses with centers located on the x-axis:
for
0 ≤ u < 1. The Fisher-Rao geodesics are semi-ellipses with centers located on the x-axis:

 μ = {N(μ,Σ) : Σ ∈
μ = {N(μ,Σ) : Σ ∈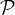 (d)}⊂
(d)}⊂ of normal
distributions sharing the same mean μ, we have:
of normal
distributions sharing the same mean μ, we have: 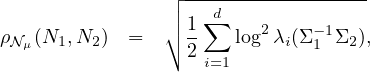
 μ,gFisher) is totally geodesic in
(
μ,gFisher) is totally geodesic in
( ,gFisher).
,gFisher).
 Σ = {N(μ,Σ) : Σ ∈
Σ = {N(μ,Σ) : Σ ∈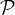 (d)}⊂
(d)}⊂ of normal
distributions sharing the same covariance matrix Σ we have
of normal
distributions sharing the same covariance matrix Σ we have
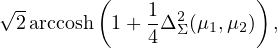
where ΔΣ is the Mahalanobis distance:
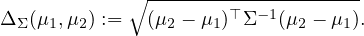
However, in the general case, the Fisher-Rao distance between normals is not known in closed form.
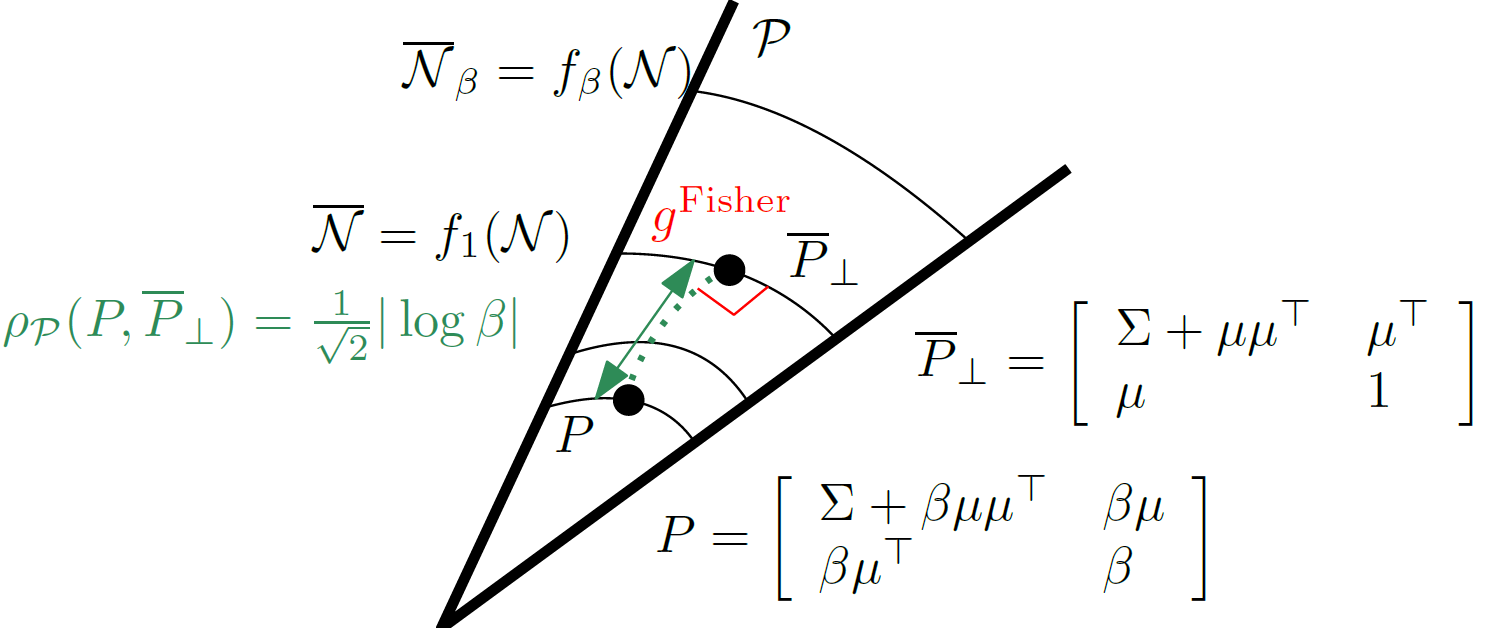
Calvo and Oller show how to embed N(μ,Σ) ∈ (d) =
(d) =  into a
SPD matrix of ℙ(d + 1):
into a
SPD matrix of ℙ(d + 1):
![[ ⊤ ]
P¯(N) = f(N ) = Σ +⊤ μμ μ
μ 1](webFisherRaoMVN14x.png)
so that the manifold ( (d),gFisher) is isometrically embedded into the submanifold (
(d),gFisher) is isometrically embedded into the submanifold ( ,gtrace) of the cone
equipped with the trace metric
,gtrace) of the cone
equipped with the trace metric
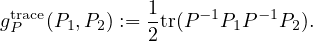
However, the submanifold  ⊂ ℙ(d + 1) is not totally geodesic. Thus Calvo and Oller derived a lower bound
on the Fisher-Rao distance:
⊂ ℙ(d + 1) is not totally geodesic. Thus Calvo and Oller derived a lower bound
on the Fisher-Rao distance:
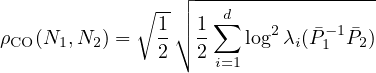
which is also metric distance.
Our method consists in projecting the SPD geodesic γℙ(d+1)(1-12) onto  and then maps back the SPD
projected curve into
and then maps back the SPD
projected curve into  by using f-1:
by using f-1:

Indeed, the geodesic γℙ(d+1)(1-12) has closed-form equation
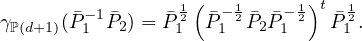
Now, we need to estimate the Fisher-Rao length of the curve cCO(N1,N2;t) by discretizing the curve at T positions:
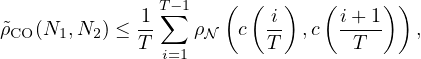
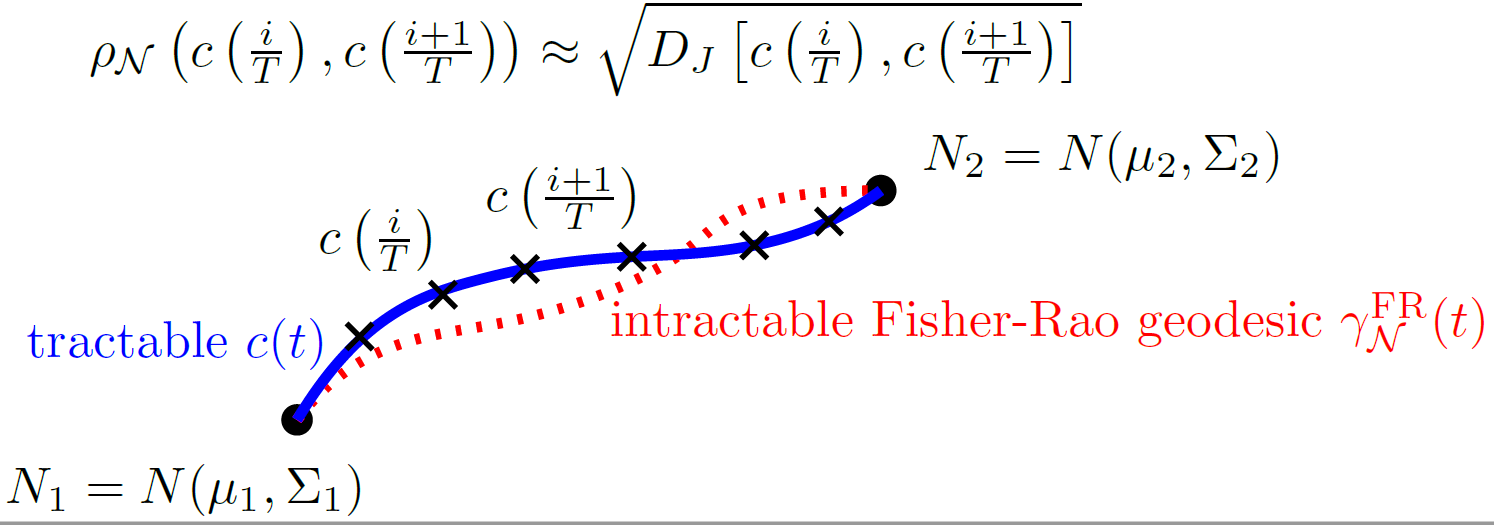
and approximate for nearby normals their Fisher-Rao distances by the square root of their Jeffreys divergence:
![( ( ) ( )) ∘ ---[-(--)---(-----)]-
ρ c -i ,c i+-1 ≈ D c i- ,c i-+1 ,
N T T J T T](webFisherRaoMVN20x.png)
where
![( -1 -1 ) -1 -1
D [p : p ] = tr Σ-2-Σ1 +-Σ-1-Σ2 - I + (μ - μ )⊤ Σ1-+-Σ-2-(μ - μ ).
J (μ1,Σ1) (μ2,Σ2) 2 2 1 2 2 1](webFisherRaoMVN21x.png)
The projection of a SPD matrix P ∈ ℙ(d + 1) onto  is done as follows: Let β = Pd+1,d+1 and write
P =
is done as follows: Let β = Pd+1,d+1 and write
P = ![[ ]
Σ+ βμ μ⊤ βμ
βμ⊤ β](webFisherRaoMVN22x.png) . Then the orthogonal projection at P ∈
. Then the orthogonal projection at P ∈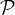 onto
onto  is:
is:
![[ ]
¯ -- Σ + μμ⊤ μ⊤
P ⊥ := projN (P) = μ 1 ,](webFisherRaoMVN23x.png)
and the SPD distance between P and ⊥ is

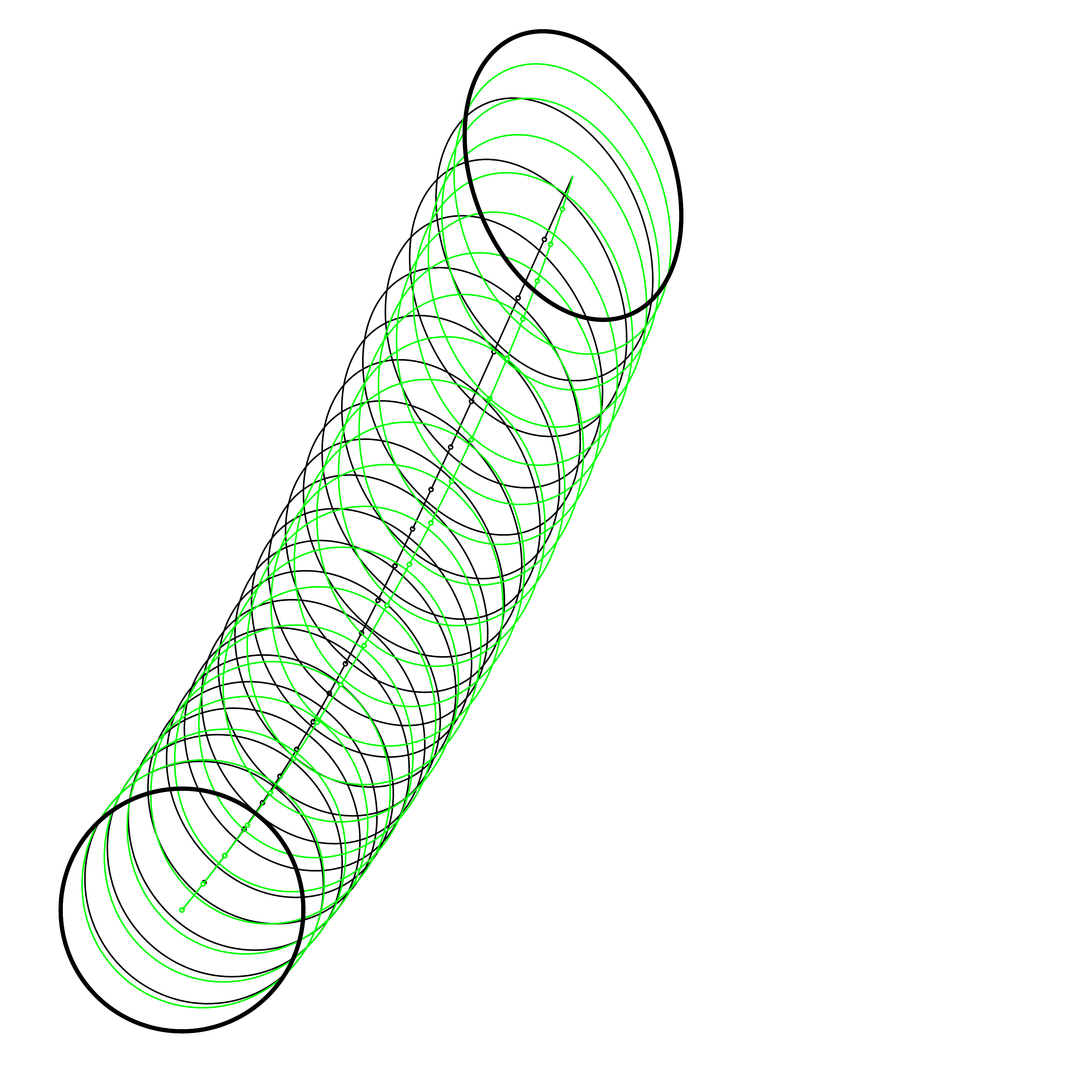
Here are some examples of the curves cCO (in green) compared to the Fisher-Rao geodesics (in black):

More details and quantitative analysis: https://www.mdpi.com/1099-4300/25/4/654