Clustering

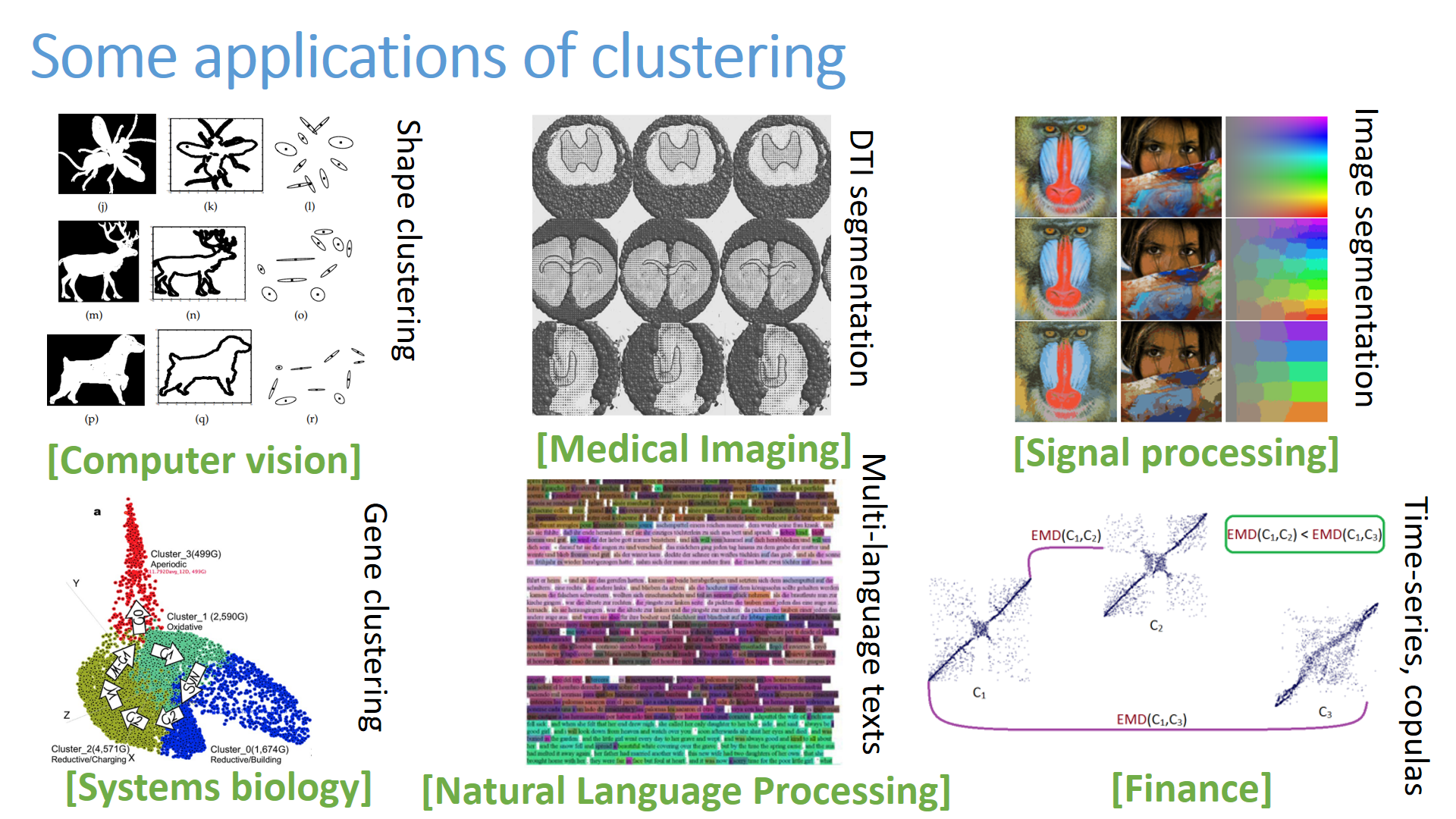
Below are some work on clustering (eg., k-means, k-center, spectral clustering, etc): Theoretical aspects and applications to computer vision, medical imaging, systems biology, financial analysis, NLP, etc.
Introduction:

Textbook chapter on k-means
Textbook chapter on hierarchical clustering

Clustering and statistics and information theory:
- Clustering in Hilbert simplex geometry
- Optimal copula transport for clustering multivariate time series, IEEE ICASSP 2016: 2379-2383
- Clustering Financial Time Series: How Long Is Enough?, IJCAI 2016: 2583-2589
- k-variates++: more pluses in the k-means++, ICML 2016
- SSSC-AM: A unified framework for video co-segmentation by structured sparse subspace clustering with appearance and motion features , IEEE ICIP 2016.
- Optimal transport vs. Fisher-Rao distance between copulas for clustering multivariate time series, IEEE SSP 2016: 1-5
- Total Jensen divergences: Definition, properties and clustering, IEEE ICASSP 2015
- On Weighting Clustering. IEEE Trans. Pattern Anal. Mach. Intell. 28(8): 1223-1235 (2006)
- Non-flat clustering with alpha-divergences, IEEE ICASSP 2011: 2100-2103
- Bhattacharyya Clustering with Applications to Mixture Simplifications, ICPR 2010: 1437-1440
- Clustering Multivariate Normal Distributions, ETVC 2008
k-means type clustering:
- On Hölder Projective Divergences,Entropy 2017, 19(3), 122; https://doi.org/10.3390/e19030122
- Optimal Interval Clustering: Application to Bregman Clustering and Statistical Mixture Learning, IEEE SPL 2014
- On Clustering Histograms with k-Means by Using Mixed α-Divergences. Entropy 16(6): 3273-3301 (2014)
- Geometry and clustering with metrics derived from separable Bregman divergences
- Further heuristics for k-means: The merge-and-split heuristic and the (k,l)-means, arXiv:1406.6314
k-center type clustering:
- On the Riemannian 1-Center, CGTA 2011
- Fitting the Smallest Enclosing Bregman Ball, ECML 2005
- On the smallest enclosing information disk, IPL 2006
Applications:
- Computer vision:
  - Shape Retrieval Using Hierarchical Total Bregman Soft Clustering, IEEE Trans. Pattern Anal. Mach. Intell. 34(12): 2407-2419 (2012)
- Medical imaging:
  - Total Bregman Divergence and Its Applications to DTI Analysis , IEEE Trans. Medical Imaging 30(2): 475-483 (2011)
- Natural languages (language text clustering):
  - Soft memberships for spectral clustering, with application to permeable language distinction
- Systems biology (gene clustering):
  - A Geometric Clustering Tool (AGCT) to robustly unravel the inner cluster structures of time-series gene expressions, PLOS One 2020
- Clustering Pareto fronts (maxima layers):
  - Clustering a 2d Pareto Front: P-center Problems Are Solvable in Polynomial Time. OLA 2020: 179-191

April 2022