Chernoff Information

• "Revisiting Chernoff Information with Likelihood Ratio Exponential Families",Entropy 2022, 24(10), 1400; https://doi.org/10.3390/e24101400
  older arXiv report 2207.03745
• Java program which performs the e-geodesic bisection search for approximating the Chernoff information between two multivariate normal distributions.
  DemoChernoffInformatioMultivariateGaussian.java (you need to install the JAMA matrix library)
  Executing the above program yields an output as follows (normal distributions are chosen randomly):

  Chernoff information of multivariate normal distributions
  Chernoff information between multivariate Gaussians
  nbiter:28
  dimension:3
  alphastar:0.6627683155238628
  nbiter:28
  Chernoff information CI:4.679592921869158
  CI Bhat cf mu sigma:4.67959292186851
  Chernoff information Bregman Divergences should be equal:4.679592917345207	4.67959293076032
  

• Closed-form Chernoff information between univariate normal distributions using Maxima
  

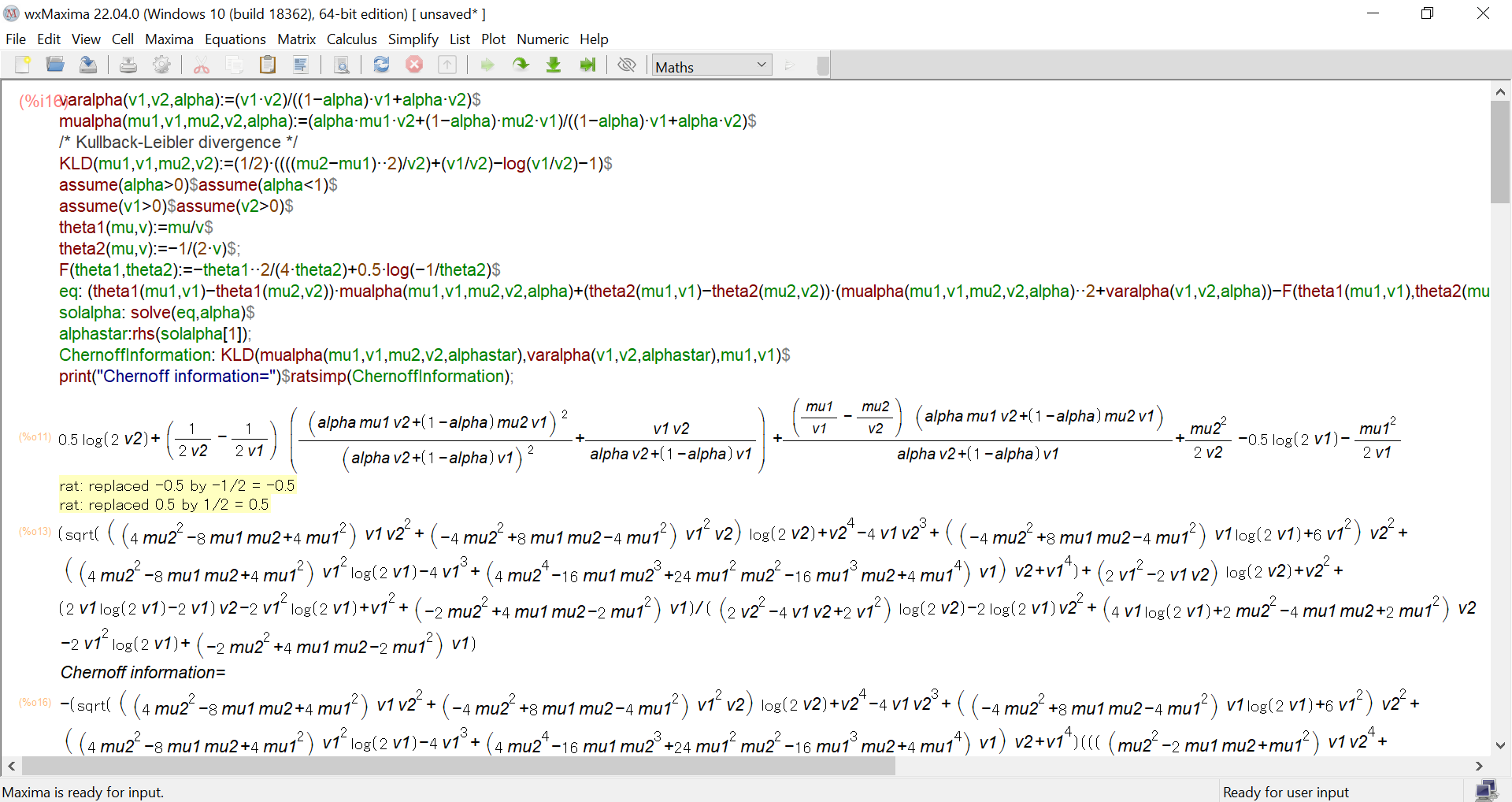
  varalpha(v1,v2,alpha):=(v1*v2)/((1-alpha)*v1+alpha*v2)$
  mualpha(mu1,v1,mu2,v2,alpha):=(alpha*mu1*v2+(1-alpha)*mu2*v1)/((1-alpha)*v1+alpha*v2)$
  /* Kullback-Leibler divergence */
  KLD(mu1,v1,mu2,v2):=(1/2)*((((mu2-mu1)**2)/v2)+(v1/v2)-log(v1/v2)-1)$
  assume(alpha>0)$assume(alpha<1)$
  assume(v1>0)$assume(v2>0)$
  theta1(mu,v):=mu/v$
  theta2(mu,v):=-1/(2*v)$;
  F(theta1,theta2):=-theta1**2/(4*theta2)+0.5*log(-1/theta2)$
  eq: (theta1(mu1,v1)-theta1(mu2,v2))*mualpha(mu1,v1,mu2,v2,alpha)+(theta2(mu1,v1)-theta2(mu2,v2))*(mualpha(mu1,v1,mu2,v2,alpha)**2+varalpha(v1,v2,alpha))-F(theta1(mu1,v1),theta2(mu1,v1))+F(theta1(mu2,v2),theta2(mu2,v2));
  solalpha: solve(eq,alpha)$
  alphastar:rhs(solalpha[1]);
  ChernoffInformation: KLD(mualpha(mu1,v1,mu2,v2,alphastar),varalpha(v1,v2,alphastar),mu1,v1)$
  print("Chernoff information=")$ratsimp(ChernoffInformation);
  

  
• Particular case of centered normal distributions with scaled covariance matrices:
  

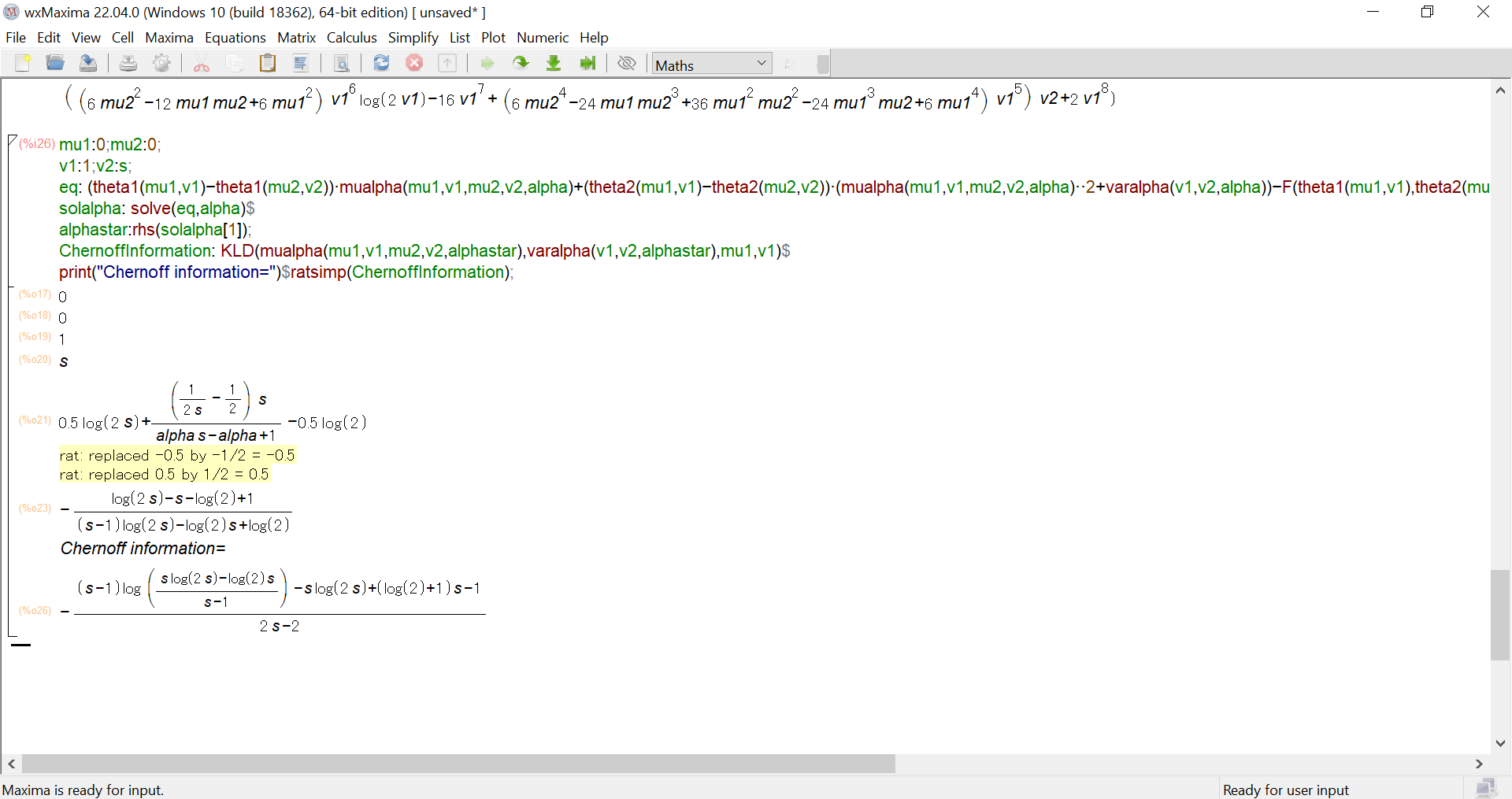
  mu1:0;mu2:0;
  v1:1;v2:s;
  eq: (theta1(mu1,v1)-theta1(mu2,v2))*mualpha(mu1,v1,mu2,v2,alpha)+(theta2(mu1,v1)-theta2(mu2,v2))*(mualpha(mu1,v1,mu2,v2,alpha)**2+varalpha(v1,v2,alpha))-F(theta1(mu1,v1),theta2(mu1,v1))+F(theta1(mu2,v2),theta2(mu2,v2));
  solalpha: solve(eq,alpha)$
  alphastar:rhs(solalpha[1]);
  ChernoffInformation: KLD(mualpha(mu1,v1,mu2,v2,alphastar),varalpha(v1,v2,alphastar),mu1,v1)$
  print("Chernoff information=")$ratsimp(ChernoffInformation);